numpy¶

../../../_images/vlado-paunovic-iBG594vhR1k-unsplash.jpg

NumPy es el paquete fundamental para computación científica en Python y manejo de arrays numéricos multi-dimensionales. 1

$ pip install numpy

La forma más común de importar esta librería es usar el alias np:

>>> import numpy as np

ndarray¶

En el núcleo de NumPy está el ndarray, donde «nd» es por n-dimensional. Un ndarray es un array multidimensional de elementos del mismo tipo.

Aquí tenemos una diferencia fundamental con las listas en Python que pueden mantener objetos heterogéneos. Y esta característica propicia que el rendimiento de un ndarray sea bastante mejor que el de una lista convencional.

Para crear un array podemos usar:

>>> import numpy as np

>>> x = np.array([1, 2, 3, 4, 5])

>>> x
array([1, 2, 3, 4, 5])

>>> type(x)
numpy.ndarray

Si queremos obtener información sobre el array creado, podemos acceder a distintos atributos del mismo:

>>> x.ndim  # dimensión
1

>>> x.size  # tamaño total del array
5

>>> x.shape  # forma
(5,)

>>> x.dtype  # tipo de sus elementos
dtype('int64')

Datos heterogéneos¶

Hemos dicho que los ndarray son estructuras de datos que almacenan un único tipo de datos. A pesar de esto, es posible crear un array con los siguientes valores:

>>> x = np.array([4, 'Einstein', 1e-7])

Aunque, a priori, puede parecer que estamos mezclando tipos enteros, flotantes y cadenas de texto, lo que realmente se produce (de forma implícita) es una coerción 2 de tipos a Unicode:

>>> x
array(['4', 'Einstein', '1e-07'], dtype='<U32')

>>> x.dtype
dtype('<U32')

Tipos de datos¶

NumPy maneja gran cantidad de tipos de datos. A diferencia de los tipos de datos numéricos en Python que no establecen un tamaño de bytes de almacenamiento, aquí sí hay una diferencia clara.

Algunos de los tipos de datos numéricos en NumPy se presentan en la siguiente tabla:

Tipos de datos numéricos en NumPy¶
dtype	Descripción	Rango
np.int32	Integer	De -2147483648 a 2147483647
np.int64	Integer	De -9223372036854775808 a 9223372036854775807
np.uint32	Unsigned integer	De 0 a 4294967295
np.uint64	Unsigned integer	De 0 a 18446744073709551615
np.float32	Float	De -3.4028235e+38 a 3.4028235e+38
np.float64	Float	De -1.7976931348623157e+308 a 1.7976931348623157e+308

Truco

NumPy entiende por defecto que int hace referencia a np.int64 y que float hace referencia a np.float64. Son «alias» bastante utilizados.

Si creamos un array de números enteros, el tipo de datos por defecto será int64:

>>> a = np.array(range(10))

>>> a
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

>>> a.dtype
dtype('int64')

Sin embargo podemos especificar el tipo de datos que nos interese:

>>> b = np.array(range(10), dtype='int32')  # 'int32' hace referencia a np.int32

>>> b
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], dtype=int32)

>>> b.dtype
dtype('int32')

Lo mismo ocurre con valores flotantes, donde float64 es el tipo de datos por defecto.

Es posible convertir el tipo de datos que almacena un array mediante el método astype. Por ejemplo:

>>> a
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

>>> c = a.astype(float)

>>> c.dtype
dtype('float64')

ndarray vs list¶

Como ya se ha comentado en la introducción de esta sección, el uso de ndarray frente a list está justificado por cuestiones de rendimiento. Pero veamos un ejemplo clarificador en el que sumamos 10 millones de valores enteros:

>>> array_as_list = list(range(int(10e6)))
>>> array_as_ndarray = np.array(array_as_list)

>>> %timeit sum(array_as_list)
48 ms ± 203 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

>>> %timeit array_as_ndarray.sum()
3.83 ms ± 4.84 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

Nota

El cómputo es casi 12 veces más rápido utilizando ndarray frente a listas clásicas.

En cualquier caso, existe la posibilidad de convertir a lista cualquier ndarray mediante el método tolist():

>>> a = np.array([10, 20, 30])

>>> a
array([10, 20, 30])

>>> b = a.tolist()

>>> b
[10, 20, 30]

>>> type(b)
list

Matrices¶

Una matriz no es más que un array bidimensional. Como ya se ha comentado, NumPy provee ndarray que se comporta como un array multidimensional con lo que podríamos crear una matriz sin mayor problema.

Veamos un ejemplo en el que tratamos de construir la siguiente matriz:

\[\begin{split}M= \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ 10 & 11 & 12 \end{bmatrix}\end{split}\]

Nos apoyamos en una lista de listas para la creación de la matriz:

>>> M = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]])

>>> M
array([[ 1,  2,  3],
       [ 4,  5,  6],
       [ 7,  8,  9],
       [10, 11, 12]])

>>> M.ndim  # bidimensional
2

>>> M.size
12

>>> M.shape  # 4 filas x 3 columnas
(4, 3)

>>> M.dtype
dtype('int64')

Ejercicio

Cree los siguientes arrays en NumPy:

\[\begin{split}\text{array1} &= \begin{bmatrix} 88 & 23 & 39 & 41 \end{bmatrix} \\ \text{array2} &= \begin{bmatrix} 76.4 & 21.7 & 38.4 \\ 41.2 & 52.8 & 68.9 \end{bmatrix}\\ \text{array3} &= \begin{bmatrix} 12 \\ 4 \\ 9 \\ 8 \end{bmatrix}\end{split}\]

Obtenga igualmente las siguientes características de cada uno de ellos: dimensión, tamaño, forma y tipo de sus elementos.

Solución: np_matrix.py

Cambiando la forma¶

Dado un array, podemos cambiar su forma mediante la función np.reshape():

>>> a = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])

>>> np.reshape(a, (3, 4))  # 3 x 4
array([[ 1,  2,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]])

Si sólo queremos especificar un número determinado de filas o columnas, podemos dejar la otra dimensión a -1:

>>> np.reshape(a, (6, -1))  # 6 filas
array([[ 1,  2],
       [ 3,  4],
       [ 5,  6],
       [ 7,  8],
       [ 9, 10],
       [11, 12]])

>>> np.reshape(a, (-1, 3))  # 3 columnas
array([[ 1,  2,  3],
       [ 4,  5,  6],
       [ 7,  8,  9],
       [10, 11, 12]])

Advertencia

En el caso de que no exista posibilidad de cambiar la forma del array por el número de filas y/o columnas especificado, obtendremos un error de tipo ValueError: cannot reshape array.

Almacenando arrays¶

Es posible que nos interese almacenar (de forma persistente) los arrays que hemos ido creando. Para ello NumPy nos provee, al menos, de dos mecanismos:

Almacenamiento en formato binario propio:

Mediante el método save() podemos guardar la estructura de datos en ficheros .npy. Veamos un ejemplo:

>>> M
array([[ 1,  2,  3],
       [ 4,  5,  6],
       [ 7,  8,  9],
       [10, 11, 12]])

>>> np.save('my_matrix', M)

>>> !ls my_matrix.npy
my_matrix.npy

>>> M_reloaded = np.load('my_matrix.npy')

>>> M_reloaded
array([[ 1,  2,  3],
       [ 4,  5,  6],
       [ 7,  8,  9],
       [10, 11, 12]])

Almacenamiento en formato de texto plano:

NumPy proporciona el método savetxt() con el que podremos volcar la estructura de datos a un fichero de texto csv. Veamos un ejemplo:

>>> M
array([[ 1,  2,  3],
       [ 4,  5,  6],
       [ 7,  8,  9],
       [10, 11, 12]])

>>> np.savetxt('my_matrix.csv', M, fmt='%d')

>>> !cat my_matrix.csv
1 2 3
4 5 6
7 8 9
10 11 12

>>> M_reloaded = np.loadtxt('my_matrix.csv', dtype=int)

>>> M_reloaded
array([[ 1,  2,  3],
       [ 4,  5,  6],
       [ 7,  8,  9],
       [10, 11, 12]])

Truco

Por defecto el almacenamiento y la carga de arrays en formato texto usa tipos de datos flotantes. Es por ello que hemos usado el parámetro fmt en el almacenamiento y el parámetro dtype en la carga.

Es posible cargar un array desempaquetando sus valores a través del parámetro unpack. En el siguiente ejemplo separamos las columnas en tres variables diferentes:

>>> M
array([[ 1,  2,  3],
       [ 4,  5,  6],
       [ 7,  8,  9],
       [10, 11, 12]])

>>> col1, col2, col3 = np.loadtxt('my_matrix.csv', unpack=True, dtype=int)

>>> col1
array([ 1,  4,  7, 10])
>>> col2
array([ 2,  5,  8, 11])
>>> col3
array([ 3,  6,  9, 12])

Funciones predefinidas para creación de arrays¶

NumPy ofrece una gran variedad de funciones predefinidas para creación de arrays que nos permiten simplificar el proceso de construcción de este tipo de estructuras de datos.

Valores fijos¶

A continuación veremos una serie de funciones para crear arrays con valores fijos.

Ceros¶

>>> np.zeros((3, 4))
array([[0., 0., 0., 0.],
       [0., 0., 0., 0.],
       [0., 0., 0., 0.]])

Por defecto, ésta y otras funciones del estilo, devuelven valores flotantes. Si quisiéramos trabajar con valores enteros basta con usar el parámetro dtype:

>>> np.zeros((3, 4), dtype=int)
array([[0, 0, 0, 0],
       [0, 0, 0, 0],
       [0, 0, 0, 0]])

Existe la posibilidad de crear un array de ceros con las mismas dimensiones (y forma) que otro array:

>>> M = np.array([[1, 2, 3], [4, 5, 6]])

>>> M
array([[1, 2, 3],
       [4, 5, 6]])

>>> np.zeros_like(M)
array([[0, 0, 0],
       [0, 0, 0]])

Lo cual sería equivalente a pasar la «forma» del array a la función predefinida de creación de ceros:

>>> np.zeros(M.shape, dtype=int)
array([[0, 0, 0],
       [0, 0, 0]])

Unos¶

>>> np.ones((3, 4))  # también existe np.ones_like()
array([[1., 1., 1., 1.],
       [1., 1., 1., 1.],
       [1., 1., 1., 1.]])

Mismo valor¶

>>> np.full((3, 4), 7)  # también existe np.full_like()
array([[7, 7, 7, 7],
       [7, 7, 7, 7],
       [7, 7, 7, 7]])

Matriz identidad¶

>>> np.eye(5)
array([[1., 0., 0., 0., 0.],
       [0., 1., 0., 0., 0.],
       [0., 0., 1., 0., 0.],
       [0., 0., 0., 1., 0.],
       [0., 0., 0., 0., 1.]])

Matriz diagonal¶

>>> np.diag([5, 4, 3, 2, 1])
array([[5, 0, 0, 0, 0],
       [0, 4, 0, 0, 0],
       [0, 0, 3, 0, 0],
       [0, 0, 0, 2, 0],
       [0, 0, 0, 0, 1]])

Ejercicio

Cree la siguiente matriz mediante código Python:

\[\begin{split}\text{diagonal} = \begin{bmatrix} 0 & 0 & 0 & \dots & 0\\ 0 & 1 & 0 & \dots & 0\\ 0 & 0 & 2 & \dots & 0\\ \vdots & \vdots & 0 & \ddots & 0\\ 0 & 0 & 0 & \dots & 49\\ \end{bmatrix}\end{split}\]

Obtenga igualmente las siguientes características de cada uno de ellos: dimensión, tamaño, forma y tipo de sus elementos.

Solución: diag.py

Valores equiespaciados¶

A continuación veremos una serie de funciones para crear arrays con valores equiespaciados o en intervalos definidos.

Valores enteros equiespaciados¶

La función que usamos para este propósito es np.arange() cuyo comportamiento es totalmente análogo a la función «built-in» range().

Especificando límite superior:

>>> np.arange(21)
array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16,
       17, 18, 19, 20])

Especificando límite inferior y superior:

>>> np.arange(6, 60)
array([ 6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22,
       23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39,
       40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56,
       57, 58, 59])

Especificando límite inferior, superior y paso:

>>> np.arange(6, 60, 3)
array([ 6,  9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54,
       57])

Es posible especificar un paso flotante en la función arange():

>>> np.arange(6, 16, .3)
array([ 6. ,  6.3,  6.6,  6.9,  7.2,  7.5,  7.8,  8.1,  8.4,  8.7,  9. ,
        9.3,  9.6,  9.9, 10.2, 10.5, 10.8, 11.1, 11.4, 11.7, 12. , 12.3,
       12.6, 12.9, 13.2, 13.5, 13.8, 14.1, 14.4, 14.7, 15. , 15.3, 15.6,
       15.9])

Valores flotantes equiespaciados¶

La función que usamos para este propósito es np.linspace() cuyo comportamiento es «similar» a np.arange() pero para valores flotantes.

Especificando límite inferior y superior:

>>> np.linspace(6, 60)  # [6, 60] con 50 valores
array([ 6.        ,  7.10204082,  8.20408163,  9.30612245, 10.40816327,
       11.51020408, 12.6122449 , 13.71428571, 14.81632653, 15.91836735,
       17.02040816, 18.12244898, 19.2244898 , 20.32653061, 21.42857143,
       22.53061224, 23.63265306, 24.73469388, 25.83673469, 26.93877551,
       28.04081633, 29.14285714, 30.24489796, 31.34693878, 32.44897959,
       33.55102041, 34.65306122, 35.75510204, 36.85714286, 37.95918367,
       39.06122449, 40.16326531, 41.26530612, 42.36734694, 43.46938776,
       44.57142857, 45.67346939, 46.7755102 , 47.87755102, 48.97959184,
       50.08163265, 51.18367347, 52.28571429, 53.3877551 , 54.48979592,
       55.59183673, 56.69387755, 57.79591837, 58.89795918, 60.        ])

Nota

Por defecto np.linspace() genera 50 elementos.

Especificando límite inferior, superior y total de elementos:

>>> np.linspace(6, 60, 20)  # [6, 60] con 20 valores
array([ 6.        ,  8.84210526, 11.68421053, 14.52631579, 17.36842105,
       20.21052632, 23.05263158, 25.89473684, 28.73684211, 31.57894737,
       34.42105263, 37.26315789, 40.10526316, 42.94736842, 45.78947368,
       48.63157895, 51.47368421, 54.31578947, 57.15789474, 60.        ])

Importante

A diferencia de np.arange(), la función np.linspace() incluye «por defecto» el límte superior especificado.

Especificando un intervalo abierto \([a,b)\):

>>> np.linspace(6, 60, 20, endpoint=False)  # [6, 60) con 20 elementos
array([ 6. ,  8.7, 11.4, 14.1, 16.8, 19.5, 22.2, 24.9, 27.6, 30.3, 33. ,
       35.7, 38.4, 41.1, 43.8, 46.5, 49.2, 51.9, 54.6, 57.3])

Valores aleatorios¶

A continuación veremos una serie de funciones para crear arrays con valores aleatorios y distribuciones de probabilidad.

Valores aleatorios enteros¶

Valores aleatorios enteros en \([a, b)\):

>>> np.random.randint(3, 30)  # escalar
4

>>> np.random.randint(3, 30, size=9)  # vector
array([29,  7,  8, 21, 27, 23, 29, 15, 28])

>>> np.random.randint(3, 30, size=(3, 3))  # matriz
array([[24,  4, 29],
       [10, 22, 27],
       [27,  7, 20]])

Valores aleatorios flotantes¶

Por simplicidad, en el resto de ejemplos vamos a obviar la salida escalar y matriz.

Valores aleatorios flotantes en \([0, 1)\):

>>> np.random.random(9)
array([0.53836208, 0.78315275, 0.6931254 , 0.97194325, 0.01523289,
       0.47692141, 0.27653964, 0.82297655, 0.70502383])

Valores aleatorios flotantes en \([a, b)\):

>>> np.random.uniform(1, 100, size=9)
array([17.00450378, 67.08416159, 56.99930273,  9.19685998, 35.27334323,
       97.34651516, 25.89283558, 53.59685476, 72.74943888])

Distribuciones de probabilidad¶

Distribución normal:

Ejemplo en el que generamos un millón de valores usando como parámetros de la distribución \(\mu = 0, \sigma = 5\)

>>> dist = np.random.normal(0, 5, size=1_000_000)

>>> dist[:20]
array([ 2.5290643 ,  1.46577658,  1.65170437, -1.36970819, -2.24547757,
        7.19905613, -4.4666239 , -1.05505116,  2.42351298, -4.45314272,
        1.13604077, -2.85054948,  4.34589478, -2.81235743, -0.8215143 ,
        0.57796411, -2.56594122, -7.14899388,  3.49197644,  1.80691996])

>>> dist.mean()
0.004992046432131982

>>> dist.std()
4.998583810032169

Muestra aleatoria:

Ejemplo en el que generamos una muestra aleatoria de un millón de lanzamientos de una moneda:

>>> coins = np.random.choice(['head', 'tail'], size=1_000_000)

>>> coins
array(['tail', 'head', 'tail', ..., 'tail', 'head', 'tail'], dtype='<U4')

>>> sum(coins == 'head')
499874
>>> sum(coins == 'tail')
500126

Muestra aleatoria con probabilidades no uniformes:

Ejemplo en el que generamos una muestra aleatoria de un millón de lanzamientos con un dado «trucado»:

>>> # La cara del "1" tiene un 50% de probabilidades de salir
>>> dices = np.random.choice(range(1, 7), size=1_000_000, p=[.5, .1, .1, .1, .1, .1])

>>> dices
array([6, 5, 4, ..., 1, 6, 1])

>>> sum(dices == 1)
500290
>>> sum(dices == 6)
99550

Muestra aleatoria sin reemplazo:

Ejemplo en el que seleccionamos 5 principios aleatorios del Zen de Python sin reemplazo:

>>> import this
>>> import codecs

>>> zen = codecs.decode(this.s, 'rot-13').splitlines()[3:]  # https://bit.ly/3xhsucQ

>>> np.random.choice(zen, size=5, replace=False)
array(['Unless explicitly silenced.',
       "Although that way may not be obvious at first unless you're Dutch.",
       'Sparse is better than dense.',
       'If the implementation is easy to explain, it may be a good idea.',
       'Complex is better than complicated.'], dtype='<U69')

Ver también

Listado de distribuciones aleatorias que se pueden utilizar en NumPy.

Ejercicio

Cree:

Una matriz de 20 filas y 5 columnas con valores flotantes equiespaciados en el intervalo cerrado \([1, 10]\).
Un array unidimensional con 128 valores aleatorios de una distribución normal \(\mu=1, \sigma=2\).
Un array unidimensional con 15 valores aleatorios de una muestra 1, X, 2 donde la probabilidad de que gane el equipo local es del 50%, la probabilidad de que empaten es del 30% y la probabilidad de que gane el visitante es del 20%.

Solución: np_random.py

Constantes¶

Numpy proporciona una serie de constantes predefinidas que facilitan su acceso y reutilización. Veamos algunas de ellas:

>>> import numpy as np

>>> np.Inf
inf

>>> np.nan
nan

>>> np.e
2.718281828459045

>>> np.pi
3.141592653589793

Manipulando elementos¶

Los arrays multidimensionales de NumPy están indexados por unos ejes que establecen la forma en la que debemos acceder a sus elementos. Véase el siguiente diagrama:

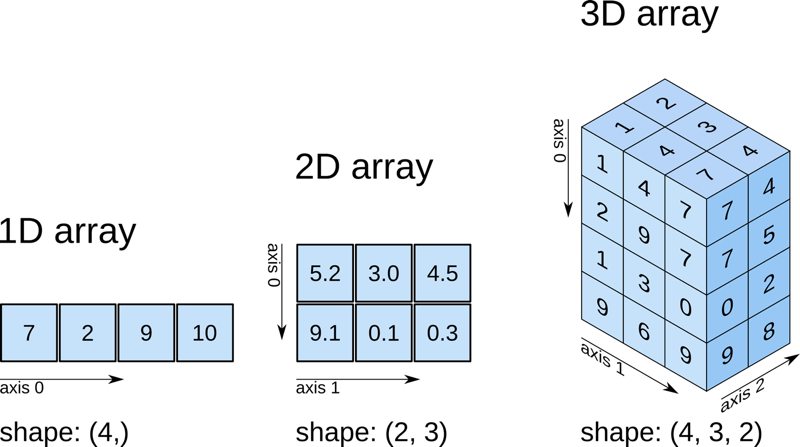
../../../_images/numpy-arrays.png — Esquema de ejes sobre los arrays de NumPy 3¶

Arrays unidimensionales¶

Acceso a arrays unidimensionales¶

>>> values
array([10, 11, 12, 13, 14, 15])

>>> values[2]
12
>>> values[-3]
13

Modificación a arrays unidimensionales¶

>>> values
array([10, 11, 12, 13, 14, 15])

>>> values[0] = values[1] + values[5]

>>> values
array([26, 11, 12, 13, 14, 15])

Borrado en arrays unidimensionales¶

>>> values
array([10, 11, 12, 13, 14, 15])

>>> np.delete(values, 2)  # índice (como escalar)
array([10, 11, 13, 14, 15])

>>> np.delete(values, (2, 3, 4))  # índices (como tupla)
array([10, 11, 15])

Nota

La función np.delete() no es destructiva. Devuelve una copia modificada del array.

Inserción en arrays unidimensionales¶

>>> values
array([10, 11, 12, 13, 14, 15])

>>> np.append(values, 16)  # añade elementos al final
array([10, 11, 12, 13, 14, 15, 16])

>>> np.insert(values, 1, 101)  # añade elementos en una posición
array([ 10, 101,  11,  12,  13,  14,  15])

Para ambas funciones también es posible añadir varios elementos de una sola vez:

>>> values
array([10, 11, 12, 13, 14, 15])

>>> np.append(values, [16, 17, 18])
array([10, 11, 12, 13, 14, 15, 16, 17, 18])

Nota

La funciones np.append() y np.insert() no son destructivas. Devuelven una copia modificada del array.

Arrays multidimensionales¶

Partimos del siguiente array bidimensional (matriz) para ejemplificar las distintas operaciones:

>>> values = np.arange(1, 13).reshape(3, 4)
>>> values
array([[ 1,  2,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]])

Acceso a arrays multidimensionales¶

>>> values
array([[ 1,  2,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]])

Acceso a elementos individuales::

>>> values[0, 0]
1
>>> values[-1, -1]
12
>>> values[1, 2]
7

Acceso a múltiples elementos::

>>> values[[0, 2], [1, 2]]  # Elementos [0, 1] y [2, 2]
array([ 2, 11])

Acceso a filas o columnas completas:

>>> values[2]  # tercera fila
array([ 9, 10, 11, 12])

>>> values[:, 1]  # segunda columna
array([ 2,  6, 10])

Acceso a zonas parciales del array:

>>> values[0:2, 0:2]
array([[1, 2],
       [5, 6]])

>>> values[0:2, [1, 3]]
array([[2, 4],
       [6, 8]])

Importante

Todos estos accesos crean una copia (vista) del array original. Esto significa que, si modificamos un valor en el array copia, se ve reflejado en el original. Para evitar esta situación podemos usar la función np.copy() y desvincular la vista de su fuente.

Modificación de arrays multidimensionales¶

>>> values
array([[ 1,  2,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]])

>>> values[0, 0] = 100

>>> values[1] = [55, 66, 77, 88]

>>> values[:,2] = [30, 70, 110]

>>> values
array([[100,   2,  30,   4],
       [ 55,  66,  70,  88],
       [  9,  10, 110,  12]])

Borrado en arrays multidimensionales¶

>>> values
array([[ 1,  2,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]])

>>> np.delete(values, 0, axis=0)  # Borrado de la primera fila
array([[ 5,  6,  7,  8],
       [ 9, 10, 11, 12]])

>>> np.delete(values, (1, 3), axis=1)  # Borrado de la segunda y cuarta columna
array([[ 1,  3],
       [ 5,  7],
       [ 9, 11]])

Truco

Tener en cuenta que axis=0 hace referencia a filas y axis=1 hace referencia a columnas tal y como describe el diagrama del comienzo de la sección.

Inserción en arrays multidimensionales¶

Añadir elementos al final del array:

>>> values
array([[1, 2],
       [3, 4]])

>>> np.append(values, [[5, 6]], axis=0)
array([[1, 2],
       [3, 4],
       [5, 6]])

>>> np.append(values, [[5], [6]], axis=1)
array([[1, 2, 5],
       [3, 4, 6]])

Insertar elementos en posiciones arbitrarias del array:

>>> values
array([[1, 2],
       [3, 4]])

>>> np.insert(values, 0, [0, 0], axis=0)
array([[0, 0],
       [1, 2],
       [3, 4]])

>>> np.insert(values, 1, [0, 0], axis=1)
array([[1, 0, 2],
       [3, 0, 4]])

Ejercicio

Utilizando las operaciones de modificación, borrado e inserción, convierta la siguiente matriz:

\[\begin{split}\begin{bmatrix} 17 & 12 & 31 \\ 49 & 11 & 51 \\ 21 & 31 & 62 \\ 63 & 75 & 22 \end{bmatrix}\end{split}\]

en esta:

\[\begin{split}\begin{bmatrix} 17 & 12 & 31 & 63\\ 49 & 11 & 51 & 75\\ 21 & 31 & 62 & 22\\ \end{bmatrix}\end{split}\]

y luego en esta:

\[\begin{split}\begin{bmatrix} 17 & 12 & 31 & 63\\ 49 & 49 & 49 & 63\\ 21 & 31 & 62 & 63\\ \end{bmatrix}\end{split}\]

Solución: np_transform.py

Apilando matrices¶

Hay veces que nos interesa combinar dos matrices (arrays en general). Una de los mecanismos que nos proporciona NumPy es el apilado.

Apilado vertical:

>>> m1 = np.random.randint(1, 100, size=(3, 2))
>>> m2 = np.random.randint(1, 100, size=(1, 2))

>>> m1
array([[68, 68],
       [10, 50],
       [87, 92]])
>>> m2
array([[63, 80]])

>>> np.vstack((m1, m2))
array([[68, 68],
       [10, 50],
       [87, 92],
       [63, 80]])

Apilado horizontal:

>>> m1 = np.random.randint(1, 100, size=(3, 2))
>>> m2 = np.random.randint(1, 100, size=(3, 1))

>>> m1
array([[51, 50],
      [52, 15],
      [14, 21]])
>>> m2
array([[18],
       [52],
       [ 1]])

>>> np.hstack((m1, m2))
array([[51, 50, 18],
       [52, 15, 52],
       [14, 21,  1]])

Repitiendo elementos¶

Repetición por ejes:

El parámetro de repetición indica el número de veces que repetimos el array completo por cada eje:

>>> values
array([[1, 2],
       [3, 4],
       [5, 6]])

>>> np.tile(values, 3)  # x3 en columnas
array([[1, 2, 1, 2, 1, 2],
       [3, 4, 3, 4, 3, 4],
       [5, 6, 5, 6, 5, 6]])

>>> np.tile(values, (2, 3))  # x2 en filas; x3 en columnas
array([[1, 2, 1, 2, 1, 2],
       [3, 4, 3, 4, 3, 4],
       [5, 6, 5, 6, 5, 6],
       [1, 2, 1, 2, 1, 2],
       [3, 4, 3, 4, 3, 4],
       [5, 6, 5, 6, 5, 6]])

Repetición por elementos:

El parámetro de repetición indica el número de veces que repetimos cada elemento del array:

>>> values
array([[1, 2],
       [3, 4],
       [5, 6]])

>>> np.repeat(values, 2)
array([1, 1, 2, 2, 3, 3, 4, 4, 5, 5, 6, 6])

>>> np.repeat(values, 2, axis=0)  # x2 en filas
array([[1, 2],
       [1, 2],
       [3, 4],
       [3, 4],
       [5, 6],
       [5, 6]])

>>> np.repeat(values, 3, axis=1)  # x3 en columnas
array([[1, 1, 1, 2, 2, 2],
       [3, 3, 3, 4, 4, 4],
       [5, 5, 5, 6, 6, 6]])

Acceso por diagonal¶

Es bastante común acceder a elementos de una matriz (array en general) tomando como referencia su diagonal. Para ello, NumPy nos provee de ciertos mecanismos que veremos a continuación.

Para ejemplificarlo, partiremos del siguiente array:

>>> values
array([[73, 86, 90, 20],
       [96, 55, 15, 48],
       [38, 63, 96, 95],
       [13, 87, 32, 96]])

Extracción de elementos por diagonal¶

La función np.diag() permite acceder a los elementos de un array especificando un parámetro k que indica la «distancia» con la diagonal principal:

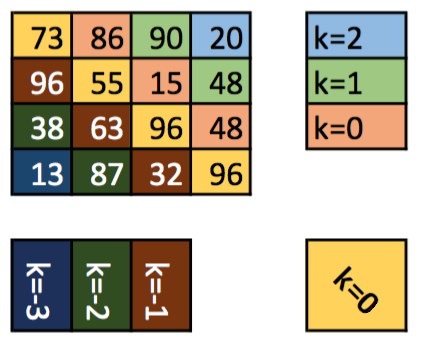
../../../_images/numpy-diagonal.png — Acceso a elementos de un array por su diagonal¶

Veamos cómo variando el parámetro k obtenemos distintos resultados:

>>> np.diag(values)  # k = 0
array([73, 55, 96, 96])

>>> for k in range(1, values.shape[0]):
...     print(f'k={k}', np.diag(values, k=k))
...
k=1 [86 15 95]
k=2 [90 48]
k=3 [20]

>>> for k in range(1, values.shape[0]):
...     print(f'k={-k}', np.diag(values, k=-k))
...
k=-1 [96 63 32]
k=-2 [38 87]
k=-3 [13]

Modificación de elementos por diagonal¶

NumPy también provee un método np.diag_indices() que retorna los índices de los elementos de la diagonal principal, con lo que podemos modificar sus valores directamente:

>>> values
array([[73, 86, 90, 20],
       [96, 55, 15, 48],
       [38, 63, 96, 95],
       [13, 87, 32, 96]])

>>> di = np.diag_indices(values.shape[0])

>>> di
(array([0, 1, 2, 3]), array([0, 1, 2, 3]))

>>> values[di] = 0

>>> values
array([[ 0, 86, 90, 20],
       [96,  0, 15, 48],
       [38, 63,  0, 95],
       [13, 87, 32,  0]])

Truco

Existen igualmente las funciones np.triu_indices() y np.tril_indices() para obtener los índices de la diagonal superior e inferior de una matriz.

Operaciones sobre arrays¶

Operaciones lógicas¶

Indexado booleano¶

El indexado booleano es una operación que permite conocer (a nivel de elemento) si un array cumple o no con una determinada condición:

>>> values
array([[60, 47, 34, 38],
       [43, 63, 37, 68],
       [58, 28, 31, 43],
       [32, 65, 32, 96]])

>>> values > 50  # indexado booleano
array([[ True, False, False, False],
       [False,  True, False,  True],
       [ True, False, False, False],
       [False,  True, False,  True]])

>>> values[values > 50]  # uso de máscara
array([60, 63, 68, 58, 65, 96])

>>> values[values > 50] = -1  # modificación de valores

>>> values
array([[-1, 47, 34, 38],
       [43, -1, 37, -1],
       [-1, 28, 31, 43],
       [32, -1, 32, -1]])

Las condiciones pueden ser más complejas e incorporar operadores lógicos | (or) y & (and):

>>> values
array([[60, 47, 34, 38],
       [43, 63, 37, 68],
       [58, 28, 31, 43],
       [32, 65, 32, 96]])

>>> (values < 25) | (values > 75)
array([[False, False, False, False],
       [False, False, False, False],
       [False, False, False, False],
       [False, False, False,  True]])

>>> (values > 25) & (values < 75)
array([[ True,  True,  True,  True],
       [ True,  True,  True,  True],
       [ True,  True,  True,  True],
       [ True,  True,  True, False]])

Consejo

El uso de paréntesis es obligatorio si queremos mantener la precedencia y que funcione correctamente.

Ejercicio

Extraiga todos los números impares de la siguiente matriz:

\[\begin{split}\text{values} = \begin{bmatrix} 10 & 11 & 12 & 13\\ 14 & 15 & 16 & 17\\ 18 & 19 & 20 & 21\\ \end{bmatrix}\end{split}\]

Solución: np_odds.py

Si lo que nos interesa es obtener los índices del array que satisfacen una determinada condición, NumPy nos proporciona el método where() cuyo comportamiento se ejemplifica a continuación:

>>> values
array([[60, 47, 34, 38],
       [43, 63, 37, 68],
       [58, 28, 31, 43],
       [32, 65, 32, 96]])

>>> idx = np.where(values > 50)

>>> idx
(array([0, 1, 1, 2, 3, 3]), array([0, 1, 3, 0, 1, 3]))

>>> values[idx]
array([60, 63, 68, 58, 65, 96])

Ejercicio

Partiendo de una matriz de 10 filas y 10 columnas con valores aleatorios enteros en el intervalo \([0, 100]\), realice las operaciones necesarias para obtener una matriz de las mismas dimensiones donde:

Todos los elementos de la diagonal sean 50.
Los elementos mayores que 50 tengan valor 100.
Los elementos menores que 50 tengan valor 0.

Solución: diag_transform.py

Comparando arrays¶

Dados dos arrays podemos compararlos usando el operador == del mismo modo que con cualquier otro objeto en Python. La cuestión es que el resultado se evalúa a nivel de elemento:

>>> m1 = np.array([[1, 2], [3, 4]])
>>> m3 = np.array([[1, 2], [3, 4]])

>>> m1 == m2
array([[ True,  True],
       [ True,  True]])

Si queremos comparar arrays en su totalidad, podemos hacer uso de la siguiente función:

>>> np.array_equal(m1, m2)
True

Operaciones de conjunto¶

Al igual que existen operaciones sobre conjuntos en Python, también podemos llevarlas a cabo sobre arrays en NumPy.

Unión de arrays¶

\(x \cup y\)

>>> x
array([ 9,  4, 11,  3, 14,  5, 13, 12,  7, 14])
>>> y
array([17,  9, 19,  4, 18,  4,  7, 13, 11, 10])

>>> np.union1d(x, y)
array([ 3,  4,  5,  7,  9, 10, 11, 12, 13, 14, 17, 18, 19])

Intersección de arrays¶

\(x \cap y\)

>>> x
array([ 9,  4, 11,  3, 14,  5, 13, 12,  7, 14])
>>> y
array([17,  9, 19,  4, 18,  4,  7, 13, 11, 10])

>>> np.intersect1d(x, y)
array([ 4,  7,  9, 11, 13])

Diferencia de arrays¶

\(x \setminus y\)

>>> x
array([ 9,  4, 11,  3, 14,  5, 13, 12,  7, 14])
>>> y
array([17,  9, 19,  4, 18,  4,  7, 13, 11, 10])

>>> np.setdiff1d(x, y)
array([ 3,  5, 12, 14])

Ordenación de arrays¶

En términos generales, existen dos formas de ordenar cualquier estructura de datos, una que modifica «in-situ» los valores (destructiva) y otra que devuelve «nuevos» valores (no destructiva). En el caso de NumPy también es así.

Ordenación sobre arrays unidimensionales¶

>>> values
array([23, 24, 92, 88, 75, 68, 12, 91, 94, 24,  9, 21, 42,  3, 66])

>>> np.sort(values)  # no destructivo
array([ 3,  9, 12, 21, 23, 24, 24, 42, 66, 68, 75, 88, 91, 92, 94])

>>> values.sort()  # destructivo

>>> values
array([ 3,  9, 12, 21, 23, 24, 24, 42, 66, 68, 75, 88, 91, 92, 94])

Ordenación sobre arrays multidimensionales¶

>>> values
array([[52, 23, 90, 46],
       [61, 63, 74, 59],
       [75,  5, 58, 70],
       [21,  7, 80, 52]])

>>> np.sort(values, axis=1)  # equivale a np.sort(values)
array([[23, 46, 52, 90],
       [59, 61, 63, 74],
       [ 5, 58, 70, 75],
       [ 7, 21, 52, 80]])

>>> np.sort(values, axis=0)
array([[21,  5, 58, 46],
       [52,  7, 74, 52],
       [61, 23, 80, 59],
       [75, 63, 90, 70]])

Nota

También existe values.sort(axis=1) y values.sort(axis=0) como métodos «destructivos» de ordenación.

Contando valores¶

Otra de las herramientas útiles que proporciona NumPy es la posibilidad de contar el número de valores que existen en un array en base a ciertos criterios.

Para ejemplificarlo, partiremos de un array unidimensional con valores de una distribución aleatoria uniforme en el intervalo \([1, 10]\):

>>> randomized = np.random.randint(1, 11, size=1000)

>>> randomized
array([ 7,  9,  7,  8,  3,  7,  6,  4,  3,  9,  3,  1,  6,  7, 10,  4,  8,
        1,  3,  3,  8,  5,  4,  7,  5,  8,  8,  3, 10,  1,  7, 10,  3, 10,
        2,  9,  5,  1,  2,  4,  4, 10,  5, 10,  5,  2,  5,  2, 10,  3,  4,
...

Valores únicos:

>>> np.unique(randomized)
array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10])

Valores únicos (incluyendo frecuencias):

>>> np.unique(randomized, return_counts=True)
(array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10]),
array([101,  97, 117,  94, 101,  88,  94, 110,  93, 105]))

Valores distintos de cero:

>>> np.count_nonzero(randomized)
1000

Valores distintos de cero (incluyendo condición):

>>> np.count_nonzero(randomized > 5)
490

Operaciones aritméticas¶

Una de las grandes ventajas del uso de arrays numéricos en NumPy es la posibilidad de trabajar con ellos como si fueran objetos «simples» pero sacando partido de la aritmética vectorial. Esto redunda en una mayor eficiencia y rapidez de cómputo.

Operaciones aritméticas con mismas dimensiones¶

Cuando operamos entre arrays de las mismas dimensiones, las operaciones aritméticas se realizan elemento a elemento (ocupando misma posición) y el resultado, obviamente, tiene las mismas dimensiones:

>>> m1
array([[21, 86, 45],
       [31, 36, 78],
       [31, 64, 70]])

>>> m2
array([[58, 67, 17],
       [99, 53,  9],
       [92, 42, 75]])

>>> m1 + m2
array([[ 79, 153,  62],
       [130,  89,  87],
       [123, 106, 145]])

>>> m1 - m2
array([[-37,  19,  28],
       [-68, -17,  69],
       [-61,  22,  -5]])

>>> m1 * m2
array([[1218, 5762,  765],
       [3069, 1908,  702],
       [2852, 2688, 5250]])

>>> m1 / m2  # división flotante
array([[0.36206897, 1.28358209, 2.64705882],
       [0.31313131, 0.67924528, 8.66666667],
       [0.33695652, 1.52380952, 0.93333333]])

>>> m1 // m2  # división entera
array([[0, 1, 2],
       [0, 0, 8],
       [0, 1, 0]])

Operaciones aritméticas con distintas dimensiones¶

Cuando operamos entre arrays con dimensiones diferentes, siempre y cuando se cumplan ciertas restricciones en tamaños de filas y/o columnas, lo que se produce es un «broadcasting» (o difusión) de los valores.

Suma con array «fila»:

>>> m
array([[9, 8, 1],
       [7, 6, 7]])

>>> v
array([[2, 3, 6]])

>>> m + v  # broadcasting
array([[11, 11,  7],
       [ 9,  9, 13]])

Suma con array «columna»:

>>> m
array([[9, 8, 1],
       [7, 6, 7]])

>>> v
array([[1],
       [6]])

>>> m + v  # broadcasting
array([[10,  9,  2],
       [13, 12, 13]])

Advertencia

En el caso de que no coincidan dimensiones de filas y/o columnas, NumPy no podrá ejecutar la operación y obtendremos un error ValueError: operands could not be broadcast together with shapes.

Operaciones entre arrays y escalares¶

Al igual que ocurría en los casos anteriores, si operamos con un array y un escalar, éste último será difundido para abarcar el tamaño del array:

>>> m
array([[9, 8, 1],
       [7, 6, 7]])

>>> m + 5
array([[14, 13,  6],
       [12, 11, 12]])

>>> m - 5
array([[ 4,  3, -4],
       [ 2,  1,  2]])

>>> m * 5
array([[45, 40,  5],
       [35, 30, 35]])

>>> m / 5
array([[1.8, 1.6, 0.2],
       [1.4, 1.2, 1.4]])

>>> m // 5
array([[1, 1, 0],
       [1, 1, 1]])

>>> m ** 5
array([[59049, 32768,     1],
       [16807,  7776, 16807]])

Operaciones unarias¶

Existen multitud de operaciones sobre un único array. A continuación veremos algunas de las más utilizas en NumPy.

Funciones universales¶

Las funciones universales «ufunc» son funciones que operan sobre arrays elemento a elemento. Existen muchas funciones universales definidas en Numpy, parte de ellas operan sobre dos arrays y parte sobre un único array.

Un ejemplo de algunas de estas funciones:

>>> values
array([[48.32172375, 24.89651106, 77.49724241],
       [77.81874191, 22.54051494, 65.11282444],
       [ 5.54960482, 59.06720303, 62.52817198]])

>>> np.sqrt(values)
array([[6.95138287, 4.98964037, 8.80325181],
       [8.82149318, 4.74768522, 8.06925179],
       [2.35575992, 7.68551905, 7.9074757 ]])

>>> np.sin(values)
array([[-0.93125201, -0.23403917,  0.86370435],
       [ 0.66019205, -0.52214693,  0.75824777],
       [-0.66953344,  0.58352079, -0.29903488]])

>>> np.ceil(values)
array([[49., 25., 78.],
       [78., 23., 66.],
       [ 6., 60., 63.]])

>>> np.floor(values)
array([[48., 24., 77.],
       [77., 22., 65.],
       [ 5., 59., 62.]])

>>> np.log(values)
array([[3.87788123, 3.21472768, 4.35024235],
       [4.3543823 , 3.11531435, 4.17612153],
       [1.71372672, 4.07867583, 4.13561721]])

Reduciendo el resultado¶

NumPy nos permite aplicar cualquier función sobre un array reduciendo el resultado por alguno de sus ejes. Esto abre una amplia gama de posibilidades.

A modo de ilustración, veamos un par de ejemplos con la suma y el producto:

>>> values
array([[8, 2, 7],
       [2, 0, 6],
       [6, 3, 4]])

>>> np.sum(values, axis=0)  # suma por columnas
array([16,  5, 17])

>>> np.sum(values, axis=1)  # suma por filas
array([17,  8, 13])

>>> np.prod(values, axis=0)  # producto por columnas
array([ 96,   0, 168])

>>> np.prod(values, axis=1)  # producto por filas
array([112,   0,  72])

Ejercicio

Compruebe que, para \(\theta=2\pi\) (radianes) y \(k=20\) se cumple la siguiente igualdad del producto infinito de Euler:

\[\cos\left({\frac{\theta}{2}}\right) \cdot \cos\left({\frac{\theta}{4}}\right) \cdot \cos\left({\frac{\theta}{8}}\right) \cdots = \prod_{i=1}^k \cos\left(\frac{\theta}{2^i}\right) \approx \frac{\sin(\theta)}{\theta}\]

Solución: euler_product.py

Funciones estadísticas¶

NumPy proporciona una gran cantidad de funciones estadísticas que pueden ser aplicadas sobre arrays.

Veamos algunas de ellas:

>>> dist
array([[-6.79006504, -0.01579498, -0.29182173,  0.3298951 , -5.30598975],
       [ 3.10720923, -4.09625791, -7.60624152,  2.3454259 ,  9.23399023],
       [-7.4394269 , -9.68427195,  3.04248586, -5.9843767 ,  1.536578  ],
       [ 3.33953286, -8.41584411, -9.530274  , -2.42827813, -7.34843663],
       [ 7.1508544 ,  5.51727548, -3.20216834, -5.00154367, -7.15715252]])

>>> np.mean(dist)
-2.1877878715377777

>>> np.std(dist)
5.393254994089515

>>> np.median(dist)
-3.2021683412383295

Máximos y mínimos¶

Una de las operaciones más comunes en el manejo de datos es encontrar máximos o mínimos. Para ello, disponemos de las típicas funciones con las ventajas del uso de arrays multidimensionales:

>>> values
array([[66, 54, 33, 15, 58],
       [55, 46, 39, 16, 38],
       [73, 75, 79, 25, 83],
       [81, 30, 22, 32,  8],
       [92, 25, 82, 10, 90]])

>>> np.min(values)
8

>>> np.min(values, axis=0)
array([55, 25, 22, 10,  8])
>>> np.min(values, axis=1)
array([15, 16, 25,  8, 10])

>>> np.max(values)
92

>>> np.max(values, axis=0)
array([92, 75, 82, 32, 90])
>>> np.max(values, axis=1)
array([66, 55, 83, 81, 92])

Si lo que interesa es obtener los índices de aquellos elementos con valores máximos o mínimos, podemos hacer uso de las funciones argmax() y argmin() respectivamente.

Veamos un ejemplo donde obtenemos los valores máximos por columnas (mediante sus índices):

>>> values
array([[66, 54, 33, 15, 58],
       [55, 46, 39, 16, 38],
       [73, 75, 79, 25, 83],
       [81, 30, 22, 32,  8],
       [92, 25, 82, 10, 90]])

>>> idx = np.argmax(values, axis=0)

>>> idx
array([4, 2, 4, 3, 4])

>>> values[idx, range(values.shape[1])]
array([92, 75, 82, 32, 90])

Vectorizando funciones¶

Una de las ventajas de trabajar con arrays numéricos en NumPy es sacar provecho de la optimización que se produce a nivel de la propia estructura de datos. En el caso de que queramos implementar una función propia para realizar una determinada acción, sería deseable seguir aprovechando esa característica.

Veamos un ejemplo en el que queremos realizar el siguiente cálculo entre dos matrices \(A\) y \(B\):

\[\begin{split}A_{ij} * B_{ij} = \begin{cases} A_{ij} + B_{ij} &, \text{si}\ A_{ij} > B_{ij}\\ A_{ij} - B_{ij} &, \text{si}\ A_{ij} < B_{ij}\\ 0 &, \text{e.o.c.} \end{cases}\end{split}\]

Esta función, definida en Python, quedaría tal que así:

>>> def customf(a, b):
...     if a > b:
...         return a + b
...     elif a < b:
...         return a - b
...     else:
...         return 0
...

Las dos matrices de partida tienen 9M de valores aleatorios entre -100 y 100:

>>> A = np.random.randint(-100, 100, size=(3000, 3000))
>>> B = np.random.randint(-100, 100, size=(3000, 3000))

Una primera aproximación para aplicar esta función a cada elemento de las matrices de entrada sería la siguiente:

>>> result = np.zeros_like(A)

>>> %%timeit
... for i in range(A.shape[0]):
...     for j in range(A.shape[1]):
...         result[i, j] = customf(A[i, j], B[i, j])
...
3 s ± 23.8 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

Mejorando rendimiento con funciones vectorizadas¶

Con un pequeño detalle podemos mejorar el rendimiento de la función que hemos diseñado anteriormente. Se trata de decorarla con np.vectorize con lo que estamos otorgándole un comportamiento distinto y enfocado al procesamiento de arrays numéricos:

>>> @np.vectorize
... def customf(a, b):
...     if a > b:
...         return a + b
...     elif a < b:
...         return a - b
...     else:
...         return 0
...

Dado que ahora ya se trata de una función vectorizada podemos aplicarla directamente a las matrices de entrada (aprovechamos para medir su tiempo de ejecución):

>>> %timeit customf(A, B)
1.29 s ± 7.33 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

Hemos obtenido una mejora de 2.32x con respecto al uso de funciones simples.

Truco

La mejora de rendimiento se aprecia más claramente a medida que los tamaños de las matrices (arrays) de entrada son mayores.

Consejo

El uso de funciones lambda puede ser muy útil en vectorización: np.vectorize(lambda a, b: return a + b).

Ejercicio

Cree dos matrices cuadradas de 20x20 con valores aleatorios flotantes uniformes en el intervalo \([0, 1000)\)
Vectorice una función que devuelva la media (elemento a elemento) entre las dos matrices.
Realice la misma operación que en 2) pero usando suma de matrices y división por escalar.
Compute los tiempos de ejecución de 2) y 3)

Solución: vectorize.py

Álgebra lineal¶

NumPy tiene una sección dedicada al álgebra lineal cuyas funciones pueden resultar muy interesantes según el contexto en el que estemos trabajando.

Producto de matrices¶

Si bien hemos hablado del producto de arrays elemento a elemento, NumPy nos permite hacer la multiplicación clásica de matrices:

>>> m1
array([[1, 8, 4],
       [8, 7, 1],
       [1, 3, 8]])

>>> m2
array([[1, 5, 7],
       [9, 4, 2],
       [1, 4, 2]])

>>> np.dot(m1, m2)
array([[77, 53, 31],
       [72, 72, 72],
       [36, 49, 29]])

En Python 3.5 se introdujo el operador @ que permitía implementar el método especial __matmul__() de multiplicación de matrices. NumPy lo ha desarrollado y simplifica la multiplicación de matrices de la siguiente manera:

>>> m1 @ m2
array([[77, 53, 31],
       [72, 72, 72],
       [36, 49, 29]])

Ejercicio

Compruebe que la matriz \(\begin{bmatrix}1 & 2\\3 & 5\end{bmatrix}\) satisface la ecuación matricial: \(X^2 - 6X - I = 0\) donde \(I\) es la matriz identidad de orden 2.

Solución: identity_equation.py

Determinante de una matriz¶

El cálculo del determinante es una operación muy utilizada en álgebra lineal. Lo podemos realizar en NumPy de la siguiente manera:

>>> m
array([[4, 1, 6],
       [4, 8, 8],
       [2, 1, 7]])

>>> np.linalg.det(m)
108.00000000000003

Inversa de una matriz¶

La inversa de una matriz se calcula de la siguiente manera:

>>> m
array([[4, 1, 6],
       [4, 8, 8],
       [2, 1, 7]])

>>> m_inv = np.linalg.inv(m)

>>> m_inv
array([[ 0.44444444, -0.00925926, -0.37037037],
       [-0.11111111,  0.14814815, -0.07407407],
       [-0.11111111, -0.01851852,  0.25925926]])

Una propiedad de la matriz inversa es que si la multiplicamos por la matriz de partida obtenemos la matriz identidad. Vemos que se cumple \(\mathcal{A} \cdot \mathcal{A}^{-1} = \mathcal{I}\):

>>> np.dot(m, m_inv)
array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])

Traspuesta de una matriz¶

La traspuesta de una matriz \(\mathcal{A}\) se denota por: \((\mathcal{A}^t)_{ij} = \mathcal{A}_{ji},\ 1\le i\le n,\ 1\le j\le m\), pero básicamente consiste en intercambiar filas por columnas.

Aún más fácil es computar la traspuesta de una matriz con NumPy:

>>> m
array([[1, 2, 3],
       [4, 5, 6]])

>>> m.T
array([[1, 4],
       [2, 5],
       [3, 6]])

Ejercicio

Dadas las matrices:

\[\begin{split}A= \begin{bmatrix} 1 & -2 & 1 \\ 3 & 0 & 1 \end{bmatrix} ;\ B= \begin{bmatrix} 4 & 0 & -1 \\ -2 & 1 & 0 \end{bmatrix}\end{split}\]

, compruebe que se cumplen las siguientes igualdades:

\((A + B)^t = A^t + B^t\)
\((3A)^t = 3A^t\)

Solución: transpose.py

Elevar matriz a potencia¶

En el mundo del álgebra lineal es muy frecuente recurrir a la exponenciación de matrices a a través de su producto clásico. En este sentido, NumPy nos proporciona una función para computarlo:

>>> m
array([[4, 1, 6],
       [4, 8, 8],
       [2, 1, 7]])

>>> np.linalg.matrix_power(m, 3)  # más eficiente que np.dot(m, np.dot(m, m))
array([[ 348,  250,  854],
       [ 848,  816, 2000],
       [ 310,  231,  775]])

Ejercicio

Dada la matriz \(A = \begin{bmatrix} 4 & 5 & -1 \\ -3 & -4 & 1 \\ -3 & -4 & 0 \end{bmatrix}\) calcule: \(A^2, A^3, \dots, A^{128}\)

¿Nota algo especial en los resultados?

Solución: flip_powers.py

Sistemas de ecuaciones lineales¶

NumPy también nos permite resolver sistemas de ecuaciones lineales. Para ello debemos modelar nuestro sistema a través de arrays.

Veamos un ejemplo en el que queremos resolver el siguiente sistema de ecuaciones lineales:

\[\begin{split}\begin{cases} x_1 + 2x_3 = 1\\ x_1 - x_2 = -2\\ x_2 + x_3 = -1 \end{cases} \Longrightarrow \begin{pmatrix} 1 & 0 & 2 \\ 1 & -1 & 0 \\ 0 & 1 & 1 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix}= \begin{pmatrix} 1 \\ -2 \\ -1 \end{pmatrix} \Longrightarrow \mathcal{A} \mathcal{X} = \mathcal{B}\end{split}\]

Podemos almacenar las matrices de coeficientes \(\mathcal{A}\) y \(\mathcal{B}\) de la siguiente manera:

>>> A = np.array([[1, 0, 2], [1, -1, 0], [0, 1, 1]])
>>> B = np.array([1, -2, -1]).reshape(-1, 1)

>>> A
array([[ 1,  0,  2],
       [ 1, -1,  0],
       [ 0,  1,  1]])
>>> B
array([[ 1],
       [-2],
       [-1]])

La solución al sistema viene dada por la siguiente función:

>>> np.linalg.solve(A, B)
array([[-7.],
       [-5.],
       [ 4.]])

La solución del sistema debe ser la misma que si obtenemos \(\mathcal{X} = \mathcal{A}^{-1} \cdot B\):

>>> np.dot(np.linalg.inv(A), B)
array([[-7.],
       [-5.],
       [ 4.]])

Ejercicio

Resuelva el siguiente sistema de ecuaciones lineales:

\[\begin{split}\begin{cases} 3x + 4y - z = 8\\ 5x - 2y + z = 4\\ 2x - 2y + z = 1 \end{cases}\end{split}\]

Solución: lineq.py

1: Foto original de portada por Vlado Paunovic en Unsplash.
2: Característica de los lenguajes de programación que permite, implícita o explícitamente, convertir un elemento de un tipo de datos en otro, sin tener en cuenta la comprobación de tipos.
3: Imagen de Harriet Dashnow, Stéfan van der Walt y Juan Núñez-Iglesias en O’Reilly.