matplotlib¶

matplotlib es el paquete Python más utilizado en el ámbito de la ciencia de datos para representaciones gráficas. 1
$ pip install matplotlib
La forma más común de importar esta librería es usar el alias plt de la siguiente manera:
>>> import matplotlib.pyplot as plt
Importante
Si bien podemos utilizar matplotlib en el intérprete habitual de Python, suele ser muy frecuente trabajar con esta librería mediante entornos Jupyter, ya que facilitan la visualización de los gráficos en su interfaz de usuario.
Figura¶
La figura es el elemento base sobre el que se construyen todos los gráficos en matplotlib. Veamos cómo crearla:
>>> fig = plt.figure()
>>> type(fig)
matplotlib.figure.Figure
>>> fig
<Figure size 640x480 with 0 Axes>
Podemos observar que la resolución (por defecto) de la figura es de 640x480 píxeles y que no dispone de ningún eje («0 Axes»).
Importante
El término «axes» hace referencia a un conjunto de ejes. Puede resultar confuso en español y he decidido asignar el nombre marco cuando haga referencia a «axes».
La resolución final de una figura viene determinada por su altura (height) y anchura (width) especificadas en pulgadas 2 que, a su vez, se multiplican por los puntos por pulgada o dpi. Veamos el funcionamiento:
>>> fig
<Figure size 640x480 with 0 Axes>
>>> fig.get_figwidth() # pulgadas
6.4
>>> fig.get_figheight() # pulgadas
4.8
>>> fig.get_dpi() # dots per inch
100.0
>>> fig.get_figwidth() * fig.dpi, fig.get_figheight() * fig.dpi
(640.0, 480.0)
Importante
Si utilizamos entornos de desarollo basados en Jupyter, los valores por defecto son distintos:
Ancho de figura: 6 in
Alto de figura: 4 in
DPI: 75
Resolución: 450x300 px
Por tanto, cuando creamos una figura podemos modificar los parámetros por defecto para obtener la resolución deseada:
>>> fig = plt.figure(figsize=(19.2, 10.8)) # 100 dpi
>>> fig
<Figure size 1920x1080 with 0 Axes>
>>> fig = plt.figure(figsize=(19.2, 10.8), dpi=300)
>>> fig
<Figure size 5760x3240 with 0 Axes>
Si nos interesa que cualquier figura tome unos valores concretos de resolución, podemos modificar los valores por defecto del entorno. Para ello, matplotlib hace uso de un diccionario plt.rcParams que contiene los parámetros globales de configuración. Veamos cómo modificarlo:
>>> plt.rcParams['figure.figsize']
[6.4, 4.8]
>>> plt.rcParams['figure.dpi']
100.0
>>> plt.rcParams['figure.figsize'] = (10, 5)
>>> plt.rcParams['figure.dpi'] = 300 # res. final: 3000x1500 px
>>> fig.get_figwidth()
10.0
>>> fig.get_figheight()
5.0
>>> fig.dpi
300.0
Marcos¶
Para poder empezar a graficar necesitamos tener, al menos, un marco. Utilizaremos la función add_subplot() que requiere pasar como parámetros el número de filas, el número de columnas y el marco activo:
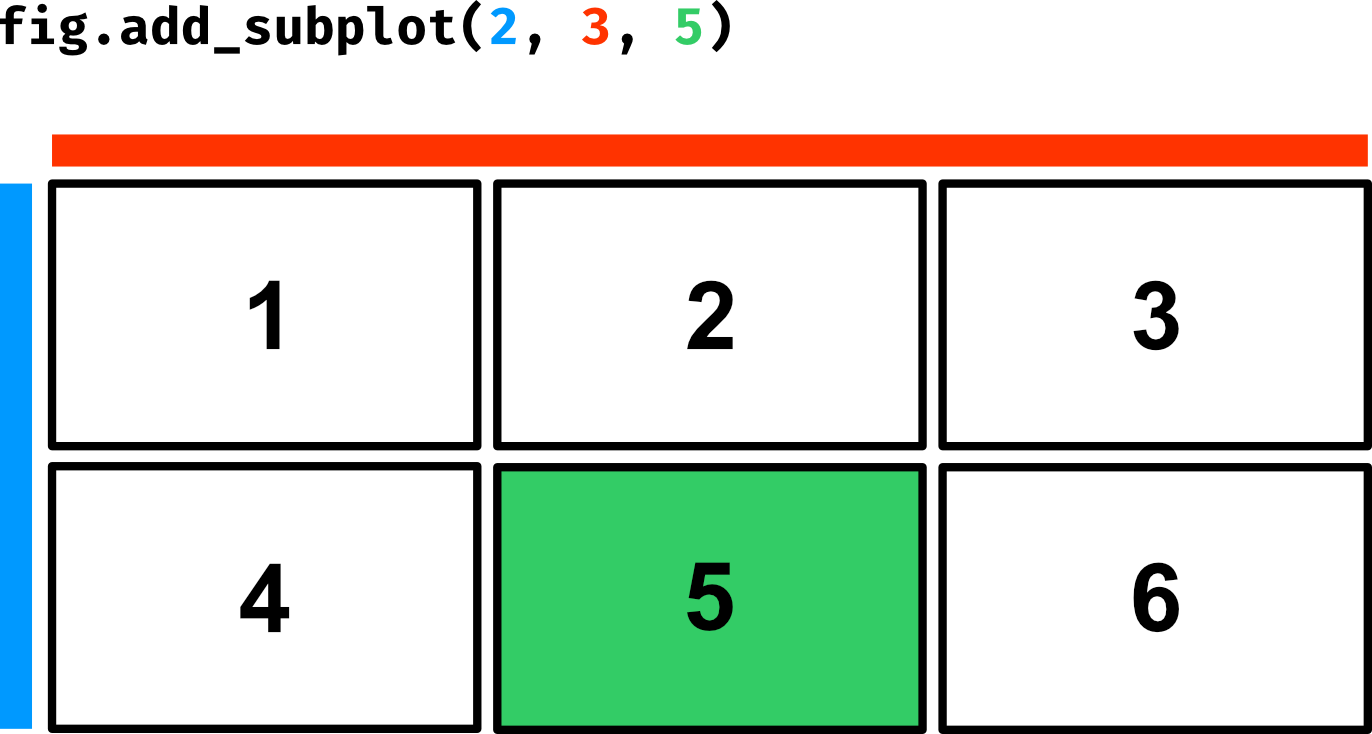
Creación de marcos dentro de una figura¶
Para comenzar vamos a trabajar únicamente con un marco:
>>> fig = plt.figure()
>>> ax = fig.add_subplot(1, 1, 1) # equivalente a fig.add_subplot(111)
>>> ax
<AxesSubplot:>
>>> fig
<Figure size 640x480 with 1 Axes>
Truco
Suele ser habitual encontrar ax como nombre de variable del «axes» devuelto por la función add_subplot().
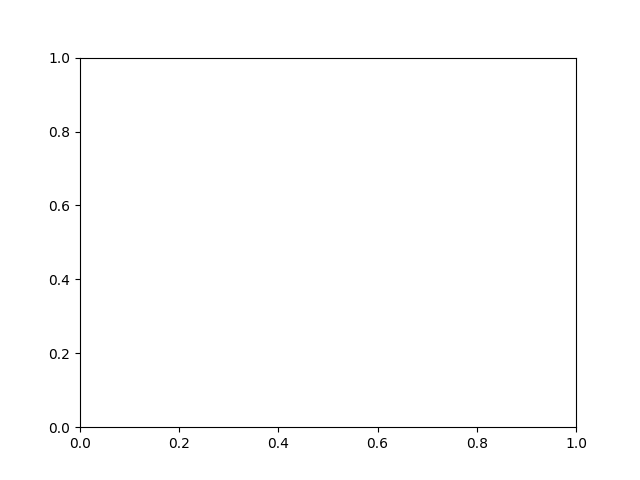
Nota
La escala por defecto de cada eje va de 0 a 1 con marcas cada 0.2
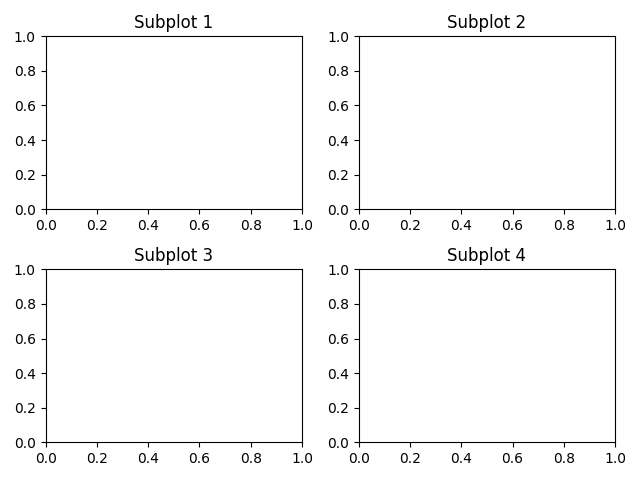
Ahora vamos a generar 4 marcos sobre los que fijaremos un título identificativo:
>>> fig = plt.figure()
>>> for i in range(1, 5):
... ax = fig.add_subplot(2, 2, i)
... ax.set_title(f'Subplot {i}')
>>> fig.tight_layout(pad=1) # sólo para que no se solapen los títulos
>>> fig
<Figure size 640x480 with 4 Axes>
Atajo para subgráficos¶
Matplotlib nos ofrece una forma compacta de crear a la vez tanto la figura como los marcos que necesitemos.
Para ello utilizaremos la función plt.subplots() que recibe como parámetros el número de filas y el número de columnas para la disposición de los marcos, y devuelve una tupla con la figura y los marcos.
En el siguiente ejemplo creamos una figura con un único marco:
>>> fig, ax = plt.subplots(1, 1)
>>> fig
<Figure size 640x480 with 1 Axes>
>>> ax
<AxesSubplot:>
Truco
Si invocamos la función plt.subplots() sin parámetros, creará (por defecto) un único marco.
En el siguiente ejemplo creamos una figura con 6 marcos en disposición de 2 filas por 3 columnas:
>>> fig, ax = plt.subplots(2, 3)
>>> fig
<Figure size 640x480 with 6 Axes>
>>> ax
array([[<AxesSubplot:>, <AxesSubplot:>, <AxesSubplot:>],
[<AxesSubplot:>, <AxesSubplot:>, <AxesSubplot:>]], dtype=object)
>>> ax.shape
(2, 3)
Nota
Se podría ver la función subplots() como una combinación de figure() + add_subplot().
Etiquetas¶
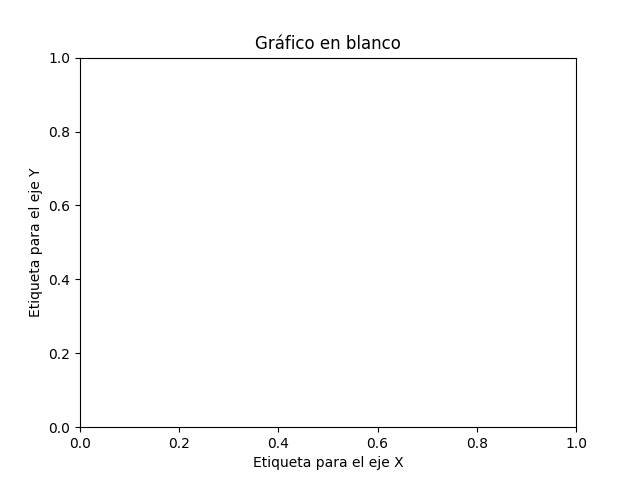
Dentro de un marco también es posible fijar las etiquetas de los ejes (X e Y). Veamos cómo hacerlo:
>>> fig, ax = plt.subplots()
>>> ax.set_title('Gráfico en blanco')
Text(0.5, 1.0, 'Gráfico en blanco')
>>> ax.set_xlabel('Etiqueta para el eje X')
Text(0.5, 0, 'Etiqueta para el eje X')
>>> ax.set_ylabel('Etiqueta para el eje Y')
Text(0, 0.5, 'Etiqueta para el eje Y')
>>> fig
<Figure size 640x480 with 1 Axes>
Ejes¶
Un marco (2D) está compuesto por dos ejes: eje X e eje Y. Podemos acceder a cada eje mediante sendos atributos:
>>> ax.xaxis
<matplotlib.axis.XAxis at 0x112b34100>
>>> ax.yaxis
<matplotlib.axis.YAxis at 0x112b34850>
Rejilla¶
En cada eje podemos activar o desactivar la rejilla, así como indicar su estilo.
En primer lugar vamos a activar la rejilla en ambos ejes:
>>> ax.xaxis.grid(True)
>>> ax.yaxis.grid(True)
Esto sería equivalente a:
>>> ax.grid(True)
Y obtendríamos una figura con la rejilla (por defecto):
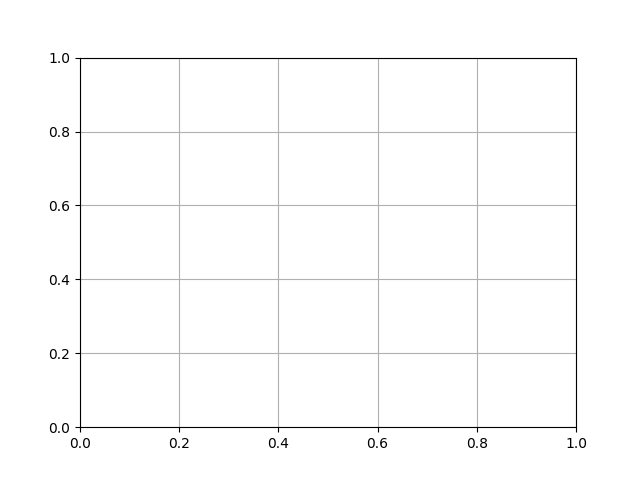
Truco
Las funciones de matplotlib que actúan como «interruptores» tienen por defecto el valor verdadero. En este sentido ax.grid() invocada sin parámetros hace que se muestre la rejilla. Esto se puede aplicar a muchas otras funciones.
Supongamos ahora que queremos personalizar la rejilla con estilos diferentes en cada eje:
>>> ax.xaxis.grid(color='r', linestyle='-') # equivale a color='red', linestyle='solid'
>>> ax.yaxis.grid(color='b', linestyle='-') # equivale a color='blue', linestyle='solid'
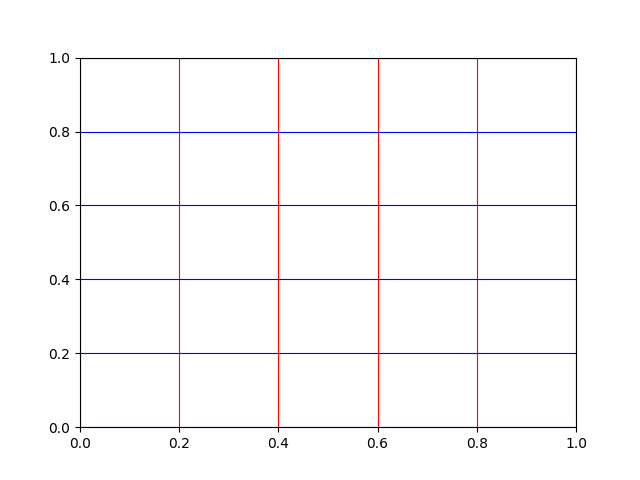
Marcas¶
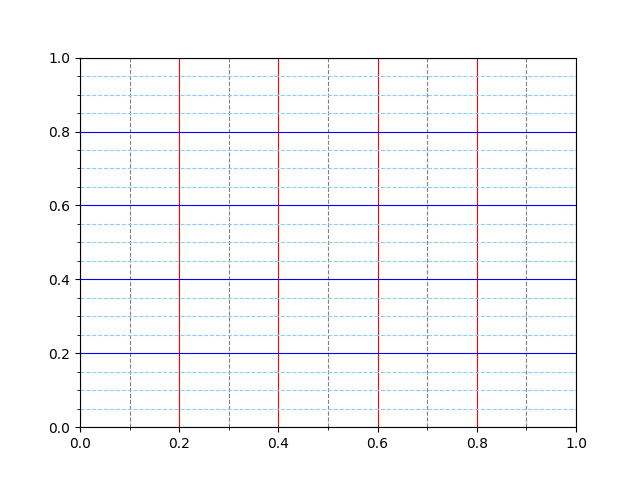
Por defecto, los ejes del marco tienen unas marcas 3 equiespaciadas que constituyen las marcas mayores. Igualmente existen unas marcas menores que, a priori, no están activadas.
Ambos elementos son susceptibles de modificarse. Veamos un ejemplo en el que establecemos las marcas menores con distinto espaciado en cada eje y además le damos un estilo diferente a cada rejilla:
>>> from matplotlib.ticker import MultipleLocator
>>> ax.xaxis.set_minor_locator(MultipleLocator(0.1)) # X: separación cada 0.1 unidades
>>> ax.yaxis.set_minor_locator(MultipleLocator(0.05)) # Y: separación cada 0.05 unidades
>>> ax.xaxis.grid(which='minor', linestyle='dashed', color='gray')
>>> ax.yaxis.grid(which='minor', linestyle='dashed', color='lightskyblue')
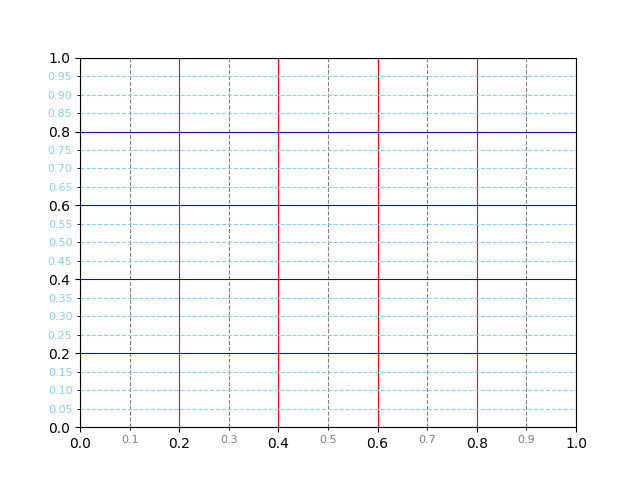
También es posible asignar etiquetas a las marcas menores. En ese sentido, veremos un ejemplo en el que incorporamos los valores a los ejes con estilos propios:
Marcas menores en el eje X: precisión de 1 decimal, tamaño de letra 8 y color gris.
Marcas menores en el eje Y: precisión de 2 decimales, tamaño de letra 8 y color azul.
>>> # Eje X
>>> ax.xaxis.set_minor_formatter('{x:.1f}')
>>> ax.tick_params(axis='x', which='minor', labelsize=8, labelcolor='gray')
>>> # Eje Y
>>> ax.yaxis.set_minor_formatter('{x:.2f}')
>>> ax.tick_params(axis='y', which='minor', labelsize=8, labelcolor='lightskyblue')
Primeros pasos¶
Vamos a empezar por representar la función \(f(x) = sin(x)\). Para ello crearemos una variable \(x\) con valores flotantes equidistantes y una variable \(y\) aplicando la función senoidal. Nos apoyamos en numpy para ello. A continuación usaremos la función plot() del marco para representar la función creada:
>>> x = np.linspace(0, 2 * np.pi)
>>> y = np.sin(x)
>>> fig, ax = plt.subplots()
>>> ax.plot(x, y)
[<matplotlib.lines.Line2D at 0x120914040>]
Múltiples funciones¶
Partiendo de un mismo marco, es posible graficar todas las funciones que necesitemos. A continuación crearemos un marco con las funciones seno y coseno:
>>> x = np.linspace(0, 2 * np.pi)
>>> sin = np.sin(x)
>>> cos = np.cos(x)
>>> fig, ax = plt.subplots()
>>> ax.plot(x, sin)
[<matplotlib.lines.Line2D at 0x1247b6310>]
>>> ax.plot(x, cos)
[<matplotlib.lines.Line2D at 0x112b0d4c0>]
Nota
Los colores «auto» asignados a las funciones siguen un ciclo establecido por matplotlib que es igualmente personalizable.
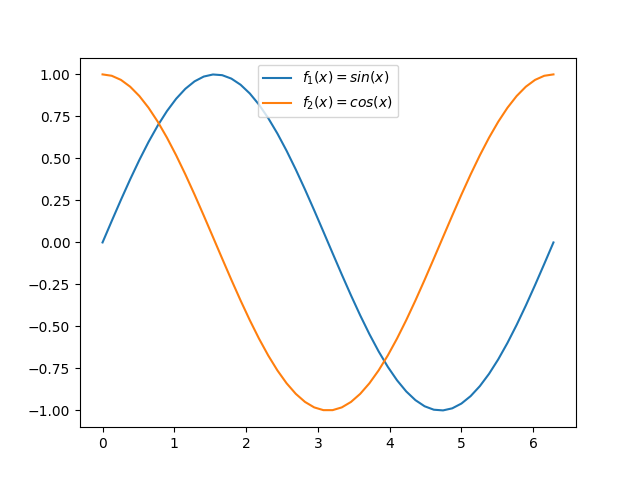
Leyenda¶
En el caso de que tengamos múltiples gráficos en el mismo marco puede ser deseable mostrar una leyenda identificativa. Para usarla necesitamos asignar etiquetas a cada función. Veamos a continuación cómo incorporar una leyenda:
>>> ax.plot(x, sin, label='sin')
[<matplotlib.lines.Line2D at 0x124e07ac0>]
>>> ax.plot(x, cos, label='cos')
[<matplotlib.lines.Line2D at 0x123c58f10>]
>>> ax.legend()
<matplotlib.legend.Legend at 0x123c8f190>
Es posible incorporar sintaxis Latex en los distintos elementos textuales de matplotlib. En el siguiente ejemplo usaremos esta notación en las etiquetas de las funciones utilizando el símbolo $ ... $ para ello:
>>> ax.plot(x, sin, label='$f_1(x) = sin(x)$')
[<matplotlib.lines.Line2D at 0x11682f3a0>]
>>> ax.plot(x, cos, label='$f_2(x) = cos(x)$')
[<matplotlib.lines.Line2D at 0x11682b3a0>]
Ubicación de la leyenda¶
Matplotlib intenta encontrar la mejor ubicación para la leyenda en el marco. Sin embargo, también es posible personalizar el lugar en el que queremos colocarla.
Si nos interesa situar la leyenda en la parte superior central del marco haríamos lo siguiente:
>>> ax.legend(loc='upper center')
<matplotlib.legend.Legend at 0x1167d43a0>
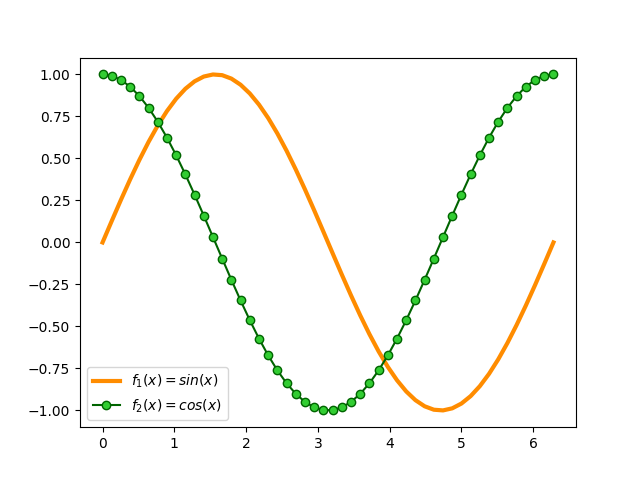
Aplicando estilos¶
Para cada función que incluimos en el marco es posible establecer un estilo personalizado con multitud de parámetros. Veamos la aplicación de algunos de estos parámetros a las funciones seno y coseno con las que hemos estado trabajando:
>>> sin_style = dict(linewidth=3, color='darkorange')
>>> cos_style = dict(marker='o', markerfacecolor='limegreen', color='darkgreen')
>>> ax.plot(x, sin, label='$f_1(x) = sin(x)$', **sin_style)
[<matplotlib.lines.Line2D at 0x1131e9fd0>]
>>> ax.plot(x, cos, label='$f_2(x) = cos(x)$', **cos_style)
[<matplotlib.lines.Line2D at 0x1226d76d0>]
Acotando ejes¶
Hay veces que nos interesa definir los límites de los ejes. En ese caso, podemos hacerlo de una manera muy sencilla:
>>> ax.set_xlim(0, np.pi / 2)
>>> ax.set_ylim(0, 1)
>>> ax.grid() # sólo a efectos estéticos
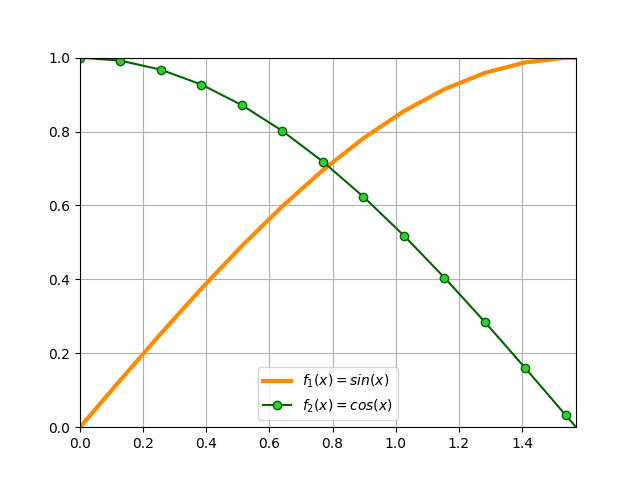
Truco
También es posible especificar únicamente límite inferior o superior en ambas funciones set_xlim() y set_ylim(). En ese caso, el otro valor sería ajustado automáticamente por matplotlib.
Anotaciones¶
En ocasiones necesitamos añadir ciertas anotaciones al gráfico que estamos diseñando. Esto permite destacar áreas o detalles que pueden ser relevantes.
Partiendo de las funciones seno y coseno con las que hemos estado trabajando, vamos a suponer que queremos obtener sus puntos de corte, es decir, resolver la siguiente ecuación:
Para el caso que nos ocupa haríamos \(n=0\) con lo que obtendríamos la siguiente solución:
>>> xsol = np.pi / 4 + np.pi * 0
>>> ysol = np.sin(xsol)
>>> xsol, ysol
(0.7853981633974483, 0.7071067811865475)
Vamos a insertar una serie de anotaciones en el gráfico:
Flecha en el punto de corte con etiqueta de ecuación.
Coordenadas de solución en el punto de corte.
Proyección del punto de corte hacia ambos ejes.
>>> ax.annotate('$sin(x) = cos(x)$',
... xy=(xsol, ysol),
... xytext=(1.2, 0.8),
... arrowprops=dict(facecolor='black', shrink=0.05))
>>> ax.text(0.47, 0.72, f'({xsol:.2f}, {ysol:.2f})')
>>> ax.plot([xsol, xsol], [0, ysol], color='gray', linestyle='--')
>>> ax.plot([0, xsol], [ysol, ysol], color='gray', linestyle='--')
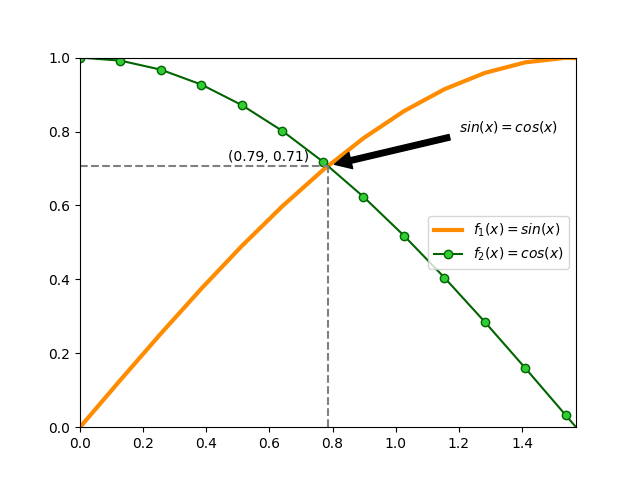
Ejercicio
Escriba el código Python necesario para obtener el siguiente gráfico:
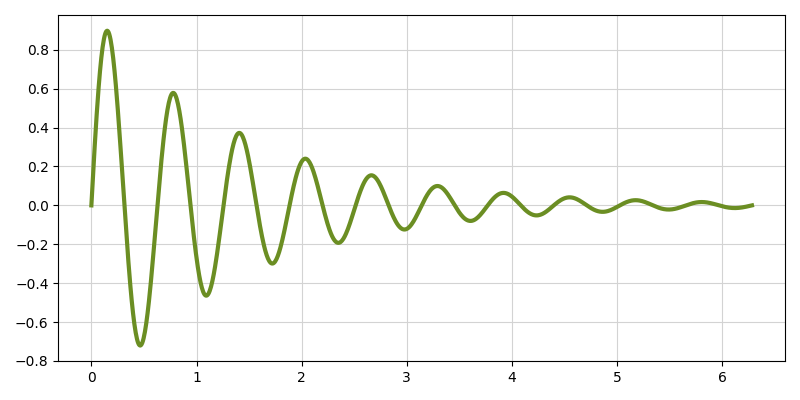
Datos:
\(x \in [0, 2\pi]\) (1000 puntos)
\(y = e^{-\alpha x} sin(\beta x)\), donde \(\alpha=0.7\) y \(\beta=10\).
Solución: soften_wave.py
Tipos de gráficos¶
Mediante matplotlib podemos hacer prácticamente cualquier tipo de gráfico. En esta sección haremos un repaso por algunos de ellos.
Gráficos de barras¶
Vamos a partir de un «dataset» que contiene los resultados de los Juegos Olímpicos de Tokio 2020. Hemos descargado el fichero medals.xlsx desde una página de Kaggle 4.
En primer lugar cargaremos este fichero en un DataFrame y haremos una pequeña «limpieza»:
>>> df = pd.read_excel('pypi/datascience/files/medals.xlsx')
>>> df.head()
Rank Team/NOC Gold Silver Bronze Total Rank by Total
0 1 United States of America 39 41 33 113 1
1 2 People's Republic of China 38 32 18 88 2
2 3 Japan 27 14 17 58 5
3 4 Great Britain 22 21 22 65 4
4 5 ROC 20 28 23 71 3
>>> df.rename(columns={'Team/NOC': 'Country'}, inplace=True)
>>> df.set_index('Country', inplace=True)
>>> df.head()
Rank Gold Silver Bronze Total Rank by Total
Country
United States of America 1 39 41 33 113 1
People's Republic of China 2 38 32 18 88 2
Japan 3 27 14 17 58 5
Great Britain 4 22 21 22 65 4
ROC 5 20 28 23 71 3
Importante
Para la carga de ficheros Excel, es necesario instalar un paquete adicional denominado openpyxl.
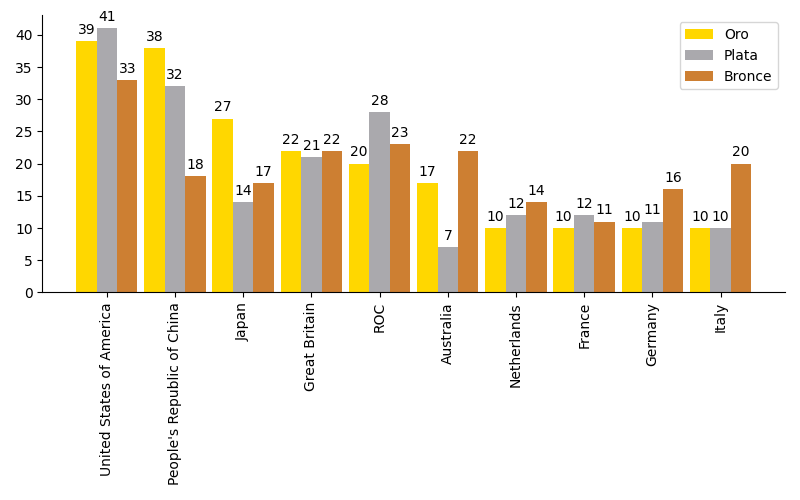
A continuación crearemos un gráfico de barras con las medallas de oro, plata y bronce de los 10 primeros países ordenados por su ranking. Lo primero será crear el subconjunto de datos sobre el que vamos a trabajar. Hay muchas maneras de hacerlo. Una de ellas:
>>> df_best = df.nsmallest(10, 'Rank')
>>> df_best
Rank Gold Silver Bronze Total Rank by Total
Country
United States of America 1 39 41 33 113 1
People's Republic of China 2 38 32 18 88 2
Japan 3 27 14 17 58 5
Great Britain 4 22 21 22 65 4
ROC 5 20 28 23 71 3
Australia 6 17 7 22 46 6
Netherlands 7 10 12 14 36 9
France 8 10 12 11 33 10
Germany 9 10 11 16 37 8
Italy 10 10 10 20 40 7
Ahora ya podemos centrarnos en el diseño del gráfico de barras:
>>> fig, ax = plt.subplots(figsize=(8, 5), dpi=100) # 800x500 px
>>> bar_width = 0.30
>>> x = np.arange(df_best.index.size)
>>> golden_medals = ax.bar(x - bar_width, df_best['Gold'],
... bar_width, label='Oro', color='#ffd700')
>>> silver_medals = ax.bar(x, df_best['Silver'],
... bar_width, label='Plata', color='#aaa9ad')
>>> bronze_medals = ax.bar(x + bar_width, df_best['Bronze'],
... bar_width, label='Bronce', color='#cd7f32')
>>> ax.set_xticks(x)
>>> ax.set_xticklabels(df_best.index, rotation=90)
>>> ax.legend()
>>> # Etiquetas en barras
>>> ax.bar_label(golden_medals, padding=3)
>>> ax.bar_label(silver_medals, padding=3)
>>> ax.bar_label(bronze_medals, padding=3)
>>> ax.spines['right'].set_visible(False) # ocultar borde derecho
>>> ax.spines['top'].set_visible(False) # ocultar borde superior
>>> fig.tight_layout() # ajustar elementos al tamaño de la figura
>>> fig
Ejercicio
Partiendo del fichero tiobe-2020-clean.csv que contiene las valoraciones de los lenguajes de programación más usados durante el año 2020 (según el índice TIOBE) 8, cree el siguiente gráfico de barras:
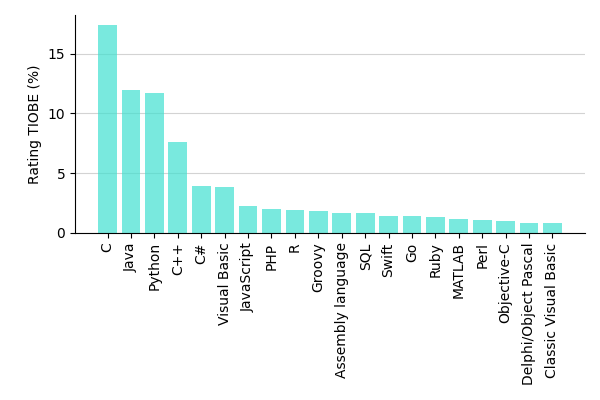
Solución: tiobe_2020.py
Gráficos de dispersión¶
Para este gráfico vamos a usar un «dataset» de jugadores de la NBA 5 extraído desde esta página de Kaggle. El fichero nba-data.csv contiene información desde 1996 hasta 2019.
En primer lugar cargamos los datos y nos quedamos con un subconjunto de las columnas:
>>> df = pd.read_csv('pypi/datascience/files/nba-data.csv', usecols=['pts', 'reb', 'ast'])
>>> df.head()
pts reb ast
0 4.8 4.5 0.5
1 0.3 0.8 0.0
2 4.5 1.6 0.9
3 7.8 4.4 1.4
4 3.7 1.6 0.5
>>> df.shape
(11700, 3)
El objetivo es crear un gráfico de dispersión en el relacionaremos los puntos anotados con los rebotes capturados, así como las asistencias dadas:
>>> fig, ax = plt.subplots(figsize=(8, 6), dpi=100) # 800x600 px
>>> # Crear variables auxiliares
>>> x = df['pts']
>>> y = df['reb']
>>> colors = df['ast']
>>> p = ax.scatter(x, y,
... s=30, # tamaño de los puntos
... c=colors, cmap='RdBu_r', # colores
... vmin=colors.min(), vmax=colors.max(), # normalización de colores
... alpha=0.7,
... edgecolors='none')
>>> # Barra de colores
>>> cb = fig.colorbar(p, ax=ax, label='Asistencias', extend='max')
>>> cb.outline.set_visible(False)
>>> ax.set_xlabel('Puntos')
>>> ax.set_ylabel('Rebotes')
>>> ax.spines['right'].set_visible(False)
>>> ax.spines['top'].set_visible(False)
>>> fig.tight_layout()
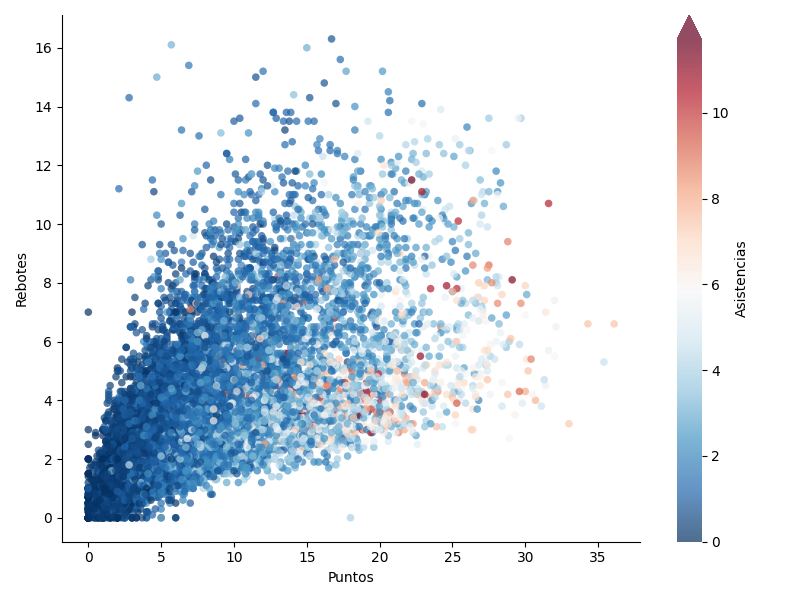
Del gráfico anterior cabe destacar varios aspectos:
Normalización: Cuando aplicamos una estética de color al gráfico basada en los datos de una variable, debemos normalizar dicha variable en el mapa de color («colormap») que elijamos. Para ello, matplotlib nos ofrece la normalización de mapas de color. En el caso concreto de
scatter()pasaríamos esta normalización mediante el parámetronormpero también podemos usar los parámetrosvminyvmax.Barra de color: Se trata de una leyenda particular en la que mostramos el gradiente de color vinculado a una determinada estética/variable del gráfico. Matplotlib también nos permite personalizar estas barras de color.
Ejercicio
Partiendo del fichero bmw-clean.csv que contiene información sobre vehículos de la marca BMW 9, cree el siguiente gráfico de dispersión:
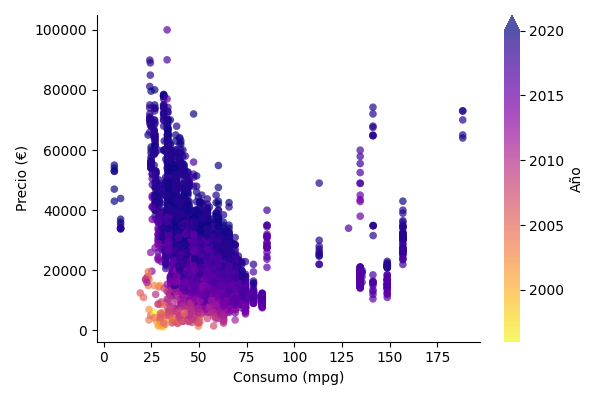
El mapa de color que se ha usado es plasma_r.
Solución: bmw_plot.py
Histogramas¶
En esta ocasión vamos a trabajar con un «dataset» de «Avengers» 6 extraído desde Kaggle. Hemos descargado el fichero avengers.csv.
Como punto de partida vamos a cargar la información y a quedarnos únicamente con la columna que hace referencia al año en el que se crearon los personajes:
>>> df = pd.read_csv('pypi/datascience/files/avengers.csv', usecols=['Year'])
>>> df.head()
Year
0 1963
1 1963
2 1963
3 1963
4 1963
>>> df.shape
(173, 1)
Igualmente haremos un pequeño filtrado para manejar sólo registros a partir de 1960:
>>> df = df[df['Year'] >= 1960]
>>> df.shape
(159, 1)
Ahora ya podemos construir el histograma, que va a representar las frecuencias absolutas de creación de personajes Marvel según su año de creación.
Aunque es posible indicar un número determinado de contenedores («bins»), en este caso vamos a especificar directamente los intervalos (cada 5 años):
>>> df['Year'].min(), df['Year'].max()
(1963, 2015)
>>> bins = range(1960, 2021, 5)
Y a continuación el código necesario para montar el gráfico:
>>> fig, ax = plt.subplots(figsize=(8, 4), dpi=100) # 800x400 px
>>> ax.hist(df,
... bins=bins, # intervalos de agrupación
... rwidth=0.95, # ancho de cada barra
... zorder=2, # barras por encima de rejilla
... color='deeppink',
... alpha=0.5)
>>> ax.spines['right'].set_visible(False)
>>> ax.spines['top'].set_visible(False)
>>> ax.set_xticks(bins) # etiquetas de intervalos en el eje x
>>> ax.yaxis.grid(color='lightgray', linestyle='--') # rejilla
>>> fig.tight_layout()
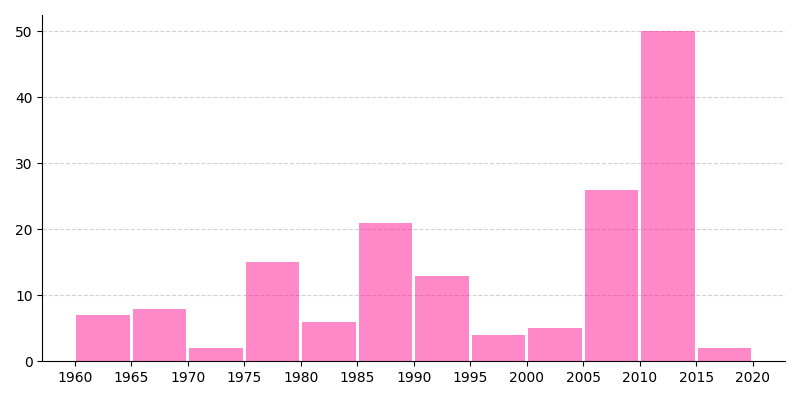
Descargo de responsabilidad: Técnicamente este gráfico no es un histograma ya que los años (fechas en general) no representan categorías válidas, pero sirve a efectos demostrativos de cómo se construyen este tipo de diagramas.
Ejercicio
Partiendo del fichero pokemon.csv que contiene información sobre Pokemon 10, cree el siguiente histograma en el que se analiza el número de personajes «pokemons» en función de su velocidad (columna Speed):
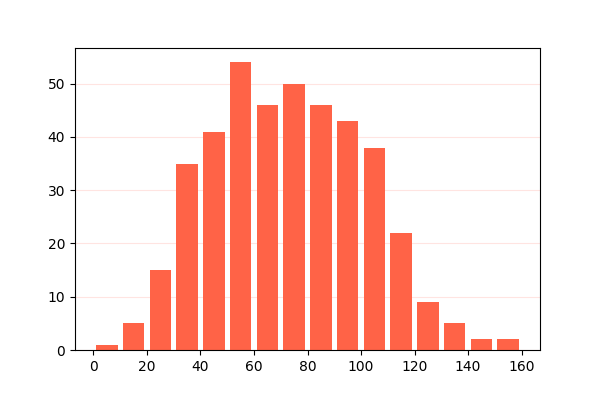
Solución: pokemon_speed.py
Gráficos para series temporales¶
Vamos a trabajar con un conjunto de datos extraído desde esta página de Kaggle que contiene información histórica de temperaturas del planeta Tierra. El fichero global-temperatures.csv se ha descargado para su tratamiento.
En primer lugar cargamos los datos, renombramos las columnas y eliminamos los valores nulos:
>>> df = pd.read_csv('pypi/datascience/files/global-temperatures.csv',
... parse_dates=['dt'], # conversión a tipo datetime
... usecols=['dt', 'LandAverageTemperature'])
>>> df.rename(columns={'dt': 'when', 'LandAverageTemperature': 'temp'}, inplace=True)
>>> df.dropna(inplace=True)
>>> df.head()
when temp
0 1750-01-01 3.034
1 1750-02-01 3.083
2 1750-03-01 5.626
3 1750-04-01 8.490
4 1750-05-01 11.573
>>> df.shape
(3180, 2)
A continuación montamos un gráfico en el que se representan todas las mediciones históricas de la temperatura media global del planeta y añadimos una línea de tendencia:
>>> # Necesitamos algunas utilidades de gestión de fechas
>>> from matplotlib.dates import YearLocator, DateFormatter, date2num
>>> from matplotlib.ticker import MultipleLocator
>>> fig, ax = plt.subplots(figsize=(8, 4), dpi=100) # 800x400 px
>>> # Alias para simplificar el acceso
>>> x = df.when
>>> y = df.temp
>>> ax.plot(x, y,
... linestyle='None', marker='.', color='tomato', # estilo de línea
... zorder=2) # orden para colocar sobre rejilla
>>> # Construcción de la línea de tendencia
>>> x = date2num(x)
>>> z = np.polyfit(x, y, 2) # ajuste polinómico de grado 2
>>> p = np.poly1d(z)
>>> plt.plot(x, p(x), linewidth=4, alpha=0.8, color='royalblue')
>>> # Formateo de los ejes
>>> ax.xaxis.set_minor_locator(YearLocator(10))
>>> ax.xaxis.set_minor_formatter(DateFormatter('%Y'))
>>> ax.tick_params(axis='x', which='minor',
... labelsize=8, labelcolor='lightgray', rotation=90)
>>> ax.xaxis.grid(which='minor', color='lightgray', linestyle='dashed')
>>> ax.yaxis.set_major_formatter('{x:.0f}º')
>>> ax.yaxis.set_minor_locator(MultipleLocator(1))
>>> ax.tick_params(axis='y', which='minor',
... labelsize=8, labelcolor='lightgray')
>>> ax.yaxis.grid(which='minor', linestyle='dashed', color='lightgray')
>>> ax.yaxis.set_minor_formatter('{x:.0f}')
>>> ax.tick_params(axis='y', which='minor', labelsize=8, labelcolor='lightgray')
>>> ax.spines['right'].set_visible(False)
>>> ax.spines['top'].set_visible(False)
>>> fig.tight_layout()
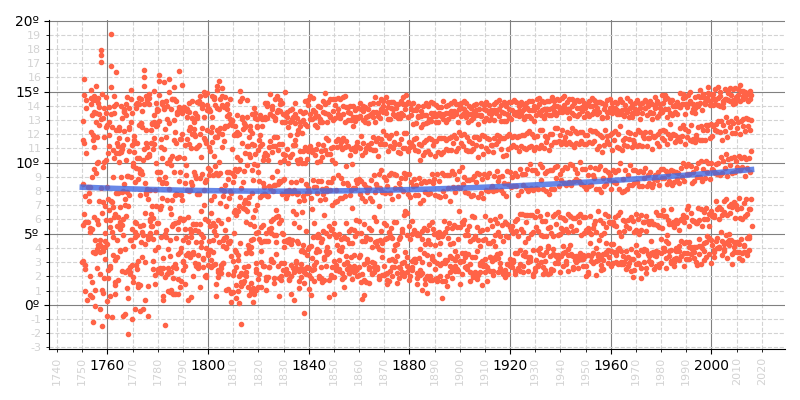
Mapas de calor¶
Para este tipo de gráfico vamos a utilizar un «dataset» que recoge las 1000 películas más valoradas en IMDB 7. Está sacado desde esta página de Kaggle y se ha descargado el fichero de datos en imdb-top-1000.csv.
En primer lugar vamos a cargar los datos quedándonos con las columnas Certificate (clasificación de la película según edades), Genre (géneros de la película) e IMDB_Rating (valoración de la película en IMDB):
>>> df = pd.read_csv('pypi/datascience/files/imdb-top-1000.csv',
... usecols=['Certificate', 'Genre', 'IMDB_Rating'])
>>> df.head()
Certificate Genre IMDB_Rating
0 A Drama 9.3
1 A Crime, Drama 9.2
2 UA Action, Crime, Drama 9.0
3 A Crime, Drama 9.0
4 U Crime, Drama 9.0
Ahora creamos una nueva columna en el DataFrame donde guardaremos únicamente el género principal de cada película:
>>> df['Main_Genre'] = df['Genre'].str.split(',', expand=True)[0]
>>> df.head()
Certificate Genre IMDB_Rating Main_Genre
0 A Drama 9.3 Drama
1 A Crime, Drama 9.2 Crime
2 UA Action, Crime, Drama 9.0 Action
3 A Crime, Drama 9.0 Crime
4 U Crime, Drama 9.0 Crime
A continuación agrupamos y obtenemos los valores medios de las valoraciones:
>>> # unstack permite disponer la agrupación en forma tabular (para el heatmap)
>>> ratings = df.groupby(['Certificate', 'Main_Genre'])['IMDB_Rating'].mean().unstack()
>>> # Nos quedamos con un subconjunto de certificados y géneros
>>> review_certificates = ['U', 'UA', 'PG-13', 'R', 'A']
>>> review_genres = ['Animation', 'Action', 'Adventure', 'Biography',
... 'Comedy', 'Crime', 'Drama']
>>> ratings = ratings.loc[review_certificates, review_genres]
>>> # Recodificamos los certificados (clasificación) con códigos más entendibles
>>> certs_description = {'U': 'ALL', 'UA': '>12', 'PG-13': '>13', 'R': '>17', 'A': '>18'}
>>> ratings.index = ratings.reset_index()['Certificate'].replace(certs_description)
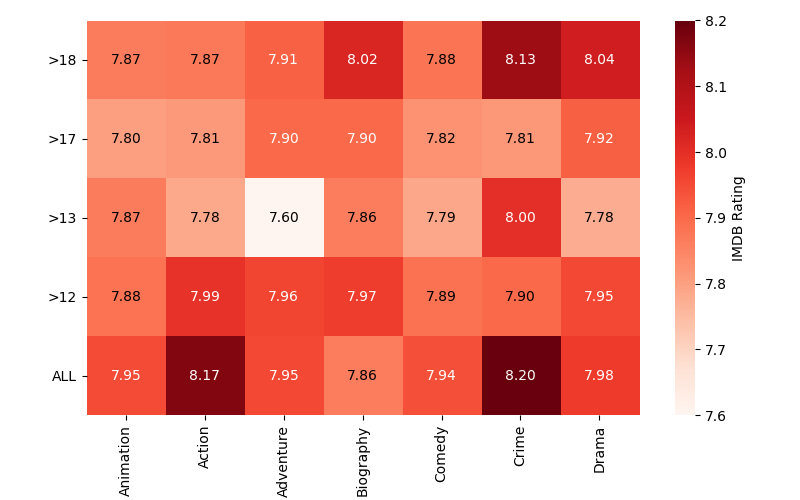
>>> ratings
Main_Genre Animation Action Adventure Biography Comedy Crime Drama
Certificate
ALL 7.947368 8.165000 7.953571 7.862500 7.940541 8.200000 7.976364
>12 7.883333 7.992424 7.958333 7.971429 7.885714 7.900000 7.953659
>13 7.866667 7.783333 7.600000 7.862500 7.785714 8.000000 7.775000
>17 7.800000 7.812500 7.900000 7.900000 7.824138 7.814286 7.915094
>18 7.866667 7.873171 7.912500 8.017647 7.877778 8.130233 8.036364
Ahora ya podemos construir el mapa de calor usando el DataFrame ratings generado previamente:
>>> fig, ax = plt.subplots(figsize=(8, 4), dpi=100)
>>> text_colors = ('black', 'white')
>>> im = ax.imshow(ratings, cmap='Reds') # mapa de calor
>>> cbar = fig.colorbar(im, ax=ax, label='IMDB Rating') # leyenda
>>> cbar.outline.set_visible(False)
>>> x = ratings.columns
>>> y = ratings.index
>>> # Mostrar las etiquetas. El color del texto cambia en función de su normalización
>>> for i in range(len(y)):
... for j in range(len(x)):
... value = ratings.iloc[i, j]
... text_color = text_colors[int(im.norm(value) > 0.5)] # color etiqueta
... ax.text(j, i, f'{value:.2f}', color=text_color, va='center', ha='center')
>>> # Formateo de los ejes
>>> ax.set_xticks(range(len(x)))
>>> ax.set_xticklabels(x, rotation=90)
>>> ax.set_yticks(range(len(y)))
>>> ax.set_yticklabels(y)
>>> ax.invert_yaxis()
>>> ax.spines[:].set_visible(False)
>>> fig.tight_layout()
Ejercicio
Partiendo del fichero euro-dollar-clean.csv que contiene información sobre el cambio euro-dollar durante los últimos 12 años 11, cree el siguiente mapa de calor en el que se analiza la evolución del cambio enfrentando meses y años:

Solución: euro_dollar.py
Diagramas de caja¶
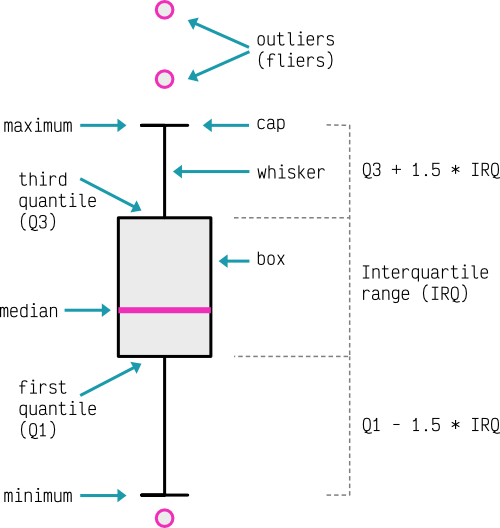
Un diagrama de caja permite visualizar la distribución de los valores de manera rápida y muy visual:
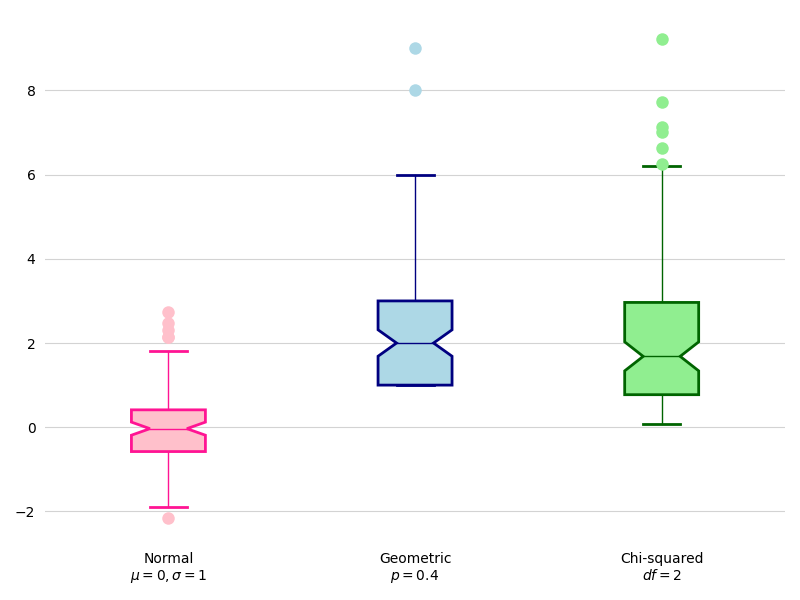
Para mostrar el funcionamiento de los diagramas de caja en Matplotlib vamos a hacer uso de distintas distribuciones aleatorias que crearemos mediante funciones de Numpy:
>>> DIST_SIZE = 100 # tamaño de la muestra
>>> boxplots = []
>>> boxplots.append(dict(
... dist=np.random.normal(0, 1, size=DIST_SIZE),
... label='Normal\n$\mu=0, \sigma=1$',
... fill_color='pink',
... brush_color='deeppink'))
>>> boxplots.append(dict(
... dist=np.random.geometric(0.4, size=DIST_SIZE),
... label='Geometric\n$p=0.4$',
... fill_color='lightblue',
... brush_color='navy'))
>>> boxplots.append(dict(
... dist=np.random.chisquare(2, size=DIST_SIZE),
... label='Chi-squared\n$df=2$',
... fill_color='lightgreen',
... brush_color='darkgreen'))
Ahora ya podemos construir el gráfico de cajas que nos permite visualizar la distribución de las muestras:
>>> fig, ax = plt.subplots(figsize=(8, 6), dpi=100) # 800x600 px
>>> for i, boxplot in enumerate(boxplots):
... fcolor, bcolor = boxplot['fill_color'], boxplot['brush_color']
... ax.boxplot(boxplot['dist'],
... labels=[boxplot['label']],
... positions=[i],
... widths=[.3],
... notch=True,
... patch_artist=True,
... boxprops=dict(edgecolor=bcolor,
... facecolor=fcolor,
... linewidth=2),
... capprops=dict(color=bcolor, linewidth=2),
... flierprops=dict(color=bcolor,
... markerfacecolor=fcolor,
... linestyle='none',
... markeredgecolor='none',
... markersize=9),
... medianprops=dict(color=bcolor),
... whiskerprops=dict(color=bcolor,
... linewidth=1))
>>> ax.yaxis.grid(color='lightgray')
>>> ax.xaxis.set_ticks_position('none')
>>> ax.yaxis.set_ticks_position('none')
>>> ax.spines[:].set_visible(False)
>>> fig.tight_layout()
Consejo
El código para preparar el gráfico se ha complicado porque se ha incidido en mejorar la estética. En cualquier caso, una vez hecho, se puede refactorizar en una función y reutilizarlo para futuros trabajos.
Gráficos de evolución¶
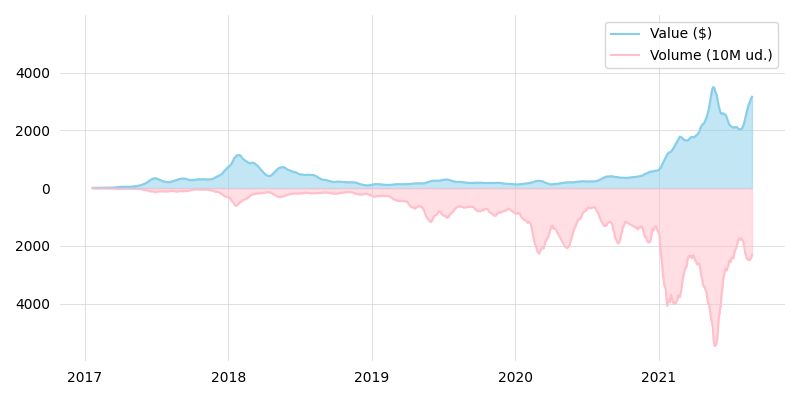
Partiendo de un conjunto de datos temporales, vamos a aprovechar para elaborar un gráfico de evolución del precio de criptomonedas. En esta ocasión hemos utilizado el «dataset» eth-usd.csv descargado desde esta página de Kaggle. Contiene la valoración de la criptomoneda Ethereum en función de una marca temporal, así como el volumen de «moneda» existente en cada momento.
El objetivo será crear un gráfico que represente el valor de la criptomoneda (a lo largo del tiempo) en contraposición al volumen de unidades.
Lo primero que haremos, además de cargar los datos, será lo siguiente:
Seleccionar las columnas Date (fecha de referencia), Open (precio de la moneda a la apertura) y Volume (volumen de moneda).
Parsear el campo fecha.
Filtrar sólo aquellos registros a partir del 1 de enero de 2017 (por simplicidad).
Dividir la columna de volumen por 10M de cara a equiparar cantidades con la valoración (ajuste de gráfico).
Aplicar una media móvil para suavizar las curvas a representar.
>>> import datetime
>>> df = pd.read_csv('pypi/datascience/files/eth-usd.csv',
... parse_dates=['Date'],
... usecols=['Date', 'Open', 'Volume'],
... index_col='Date')
>>> min_date = datetime.datetime(year=2017, month=1, day=1)
>>> df = df.loc[df.index > min_date]
>>> df['Volume'] /= 1e7
>>> df_smooth = df.rolling(20).mean().dropna()
>>> df_smooth.head()
Open Volume
Date
2017-01-21 9.968611 2.146882
2017-01-22 10.105573 2.117377
2017-01-23 10.222339 1.985587
2017-01-24 10.273270 1.821968
2017-01-25 10.239854 1.647938
Ahora ya podemos montar el gráfico dedicando algo de esfuerzo a la parte estética:
>>> fig, ax = plt.subplots(figsize=(8, 4), dpi=100) # 800x400px
>>> # Alias para facilitar el acceso
>>> x = df_smooth.index
>>> y_open = df_smooth['Open']
>>> y_vol = df_smooth['Volume']
>>> # Líneas de evolución
>>> ax.plot(x, y_open, label='Value ($)', color='skyblue', linewidth=1.5)
>>> ax.plot(x, -y_vol, label='Volume (10M ud.)', color='pink', linewidth=1.5)
>>> # Relleno del área
>>> plt.fill_between(x, y_open, alpha=0.5, color='skyblue', zorder=3)
>>> plt.fill_between(x, -y_vol, alpha=0.5, color='pink', zorder=3)
>>> # Formateo de los ejes
>>> ax.xaxis.set_ticks_position('none')
>>> ax.yaxis.set_ticks_position('none')
>>> y_ticks = [-4000, -2000, 0, 2000, 4000]
>>> y_tick_labels = ['4000', '2000', '0', '2000', '4000']
>>> ax.set_yticks(y_ticks)
>>> ax.set_yticklabels(y_tick_labels)
>>> ax.set_ylim(-6000, 6000)
>>> # Rejilla
>>> ax.xaxis.grid(color='lightgray', linewidth=.5)
>>> for y_tick in y_ticks:
... if y_tick != 0:
... ax.axhline(y_tick, color='lightgray', linewidth=.5)
>>> ax.legend()
>>> ax.spines[:].set_visible(False)
>>> fig.tight_layout()
Ejercicio
Partiendo del fichero mwh-spain-2021-clean.csv que contiene información sobre el precio de la energía en España durante el año 2021 12, cree el siguiente diagrama de evolución que representa la variación del precio del MWh 13 en función del tiempo:
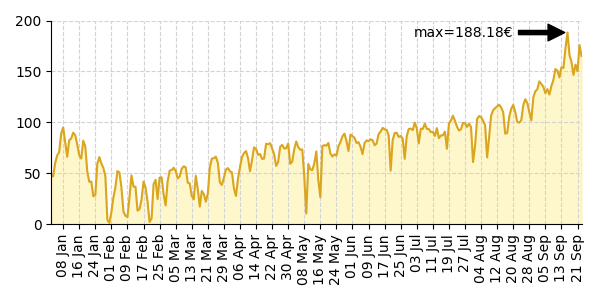
Las marcas (en el eje x) tienen una separación de 10 días.
Solución: mwh_spain.py
- 1
Foto original de portada por Customerbox en Unsplash.
- 2
Se suele usar el término inglés «inches».
- 3
Se suele usar el término inglés «ticks».
- 4
Kaggle es un servicio web que ofrece una gran variedad de «datasets», así como código, cursos y otros recursos en relación con la ciencia de datos.
- 5
National Basketball League (liga estadounidense de baloncesto).
- 6
Los Vengadores son un equipo de superhéroes publicados por Marvel Comics.
- 7
IMDB es una reconocida página web que contiene valoraciones sobre películas y series.
- 8
Datos extraídos desde esta página de Kaggle.
- 9
Datos extraídos desde esta página de Kaggle.
- 10
Datos extraídos desde esta página de Kaggle.
- 11
Datos extraídos desde esta página de Kaggle.
- 12
Datos extraídos desde esta página de El País.
- 13
Mega Watio Hora (medida de consumo de energía)
- 14
Inspirado en este artículo de Towards Data Science.