Conjuntos¶

Un conjunto en Python representa una serie de valores únicos y sin orden establecido. Mantiene muchas similitudes con el concepto matemático de conjunto 1
Creando conjuntos¶
Para crear un conjunto basta con separar sus valores por comas y rodearlos de llaves {}:
>>> lottery = {21, 10, 46, 29, 31, 94}
>>> lottery
{10, 21, 29, 31, 46, 94}
La excepción la tenemos a la hora de crear un conjunto vacío, ya que, siguiendo la lógica de apartados anteriores, deberíamos hacerlo a través de llaves:
>>> wrong_empty_set = {}
>>> type(wrong_empty_set)
dict
Advertencia
Si hacemos esto, lo que obtenemos es un diccionario vacío.
La única opción que tenemos es utilizar la función set():
>>> empty_set = set()
>>> empty_set
set()
>>> type(empty_set)
set
Advertencia
Aunque está permitido, NUNCA llames set a una variable porque destruirías la función que nos permite crear conjuntos. Y tampoco uses nombres derivados como _set o set_ ya que no son nombres representativos que identifiquen el propósito de la variable.
Conversión¶
Para convertir otros tipos de datos en un conjunto podemos usar la función set() sobre cualquier iterable:
>>> set('aplatanada')
{'a', 'd', 'l', 'n', 'p', 't'}
>>> set([1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5])
{1, 2, 3, 4, 5}
>>> set(('ADENINA', 'TIMINA', 'TIMINA', 'GUANINA', 'ADENINA', 'CITOSINA'))
{'ADENINA', 'CITOSINA', 'GUANINA', 'TIMINA'}
>>> set({'manzana': 'rojo', 'plátano': 'amarillo', 'kiwi': 'verde'})
{'kiwi', 'manzana', 'plátano'}
Importante
Como se ha visto en los ejemplos anteriores, set() se suele utilizar en muchas ocasiones como una forma de extraer los valores únicos de otros tipos de datos. En el caso de los diccionarios se extraen las claves, que, por definición, son únicas.
Nota
El hecho de que en los ejemplos anteriores los elementos de los conjuntos estén ordenados es únicamente un «detalle de implementación» en el que no se puede confiar.
Operaciones con conjuntos¶
Obtener un elemento¶
En un conjunto no existe un orden establecido para sus elementos, por lo tanto no podemos acceder a un elemento en concreto.
De este hecho se deriva igualmente que no podemos modificar un elemento existente, ya que ni siquiera tenemos acceso al mismo. Python sí nos permite añadir o borrar elementos de un conjunto.
Añadir un elemento¶
Para añadir un elemento a un conjunto debemos utilizar la función add(). Como ya hemos indicado, al no importar el orden dentro del conjunto, la inserción no establece a priori la posición donde se realizará.
A modo de ejemplo, vamos a partir de un conjunto que representa a los cuatro integrantes originales de The Beatles. Luego añadiremos a un nuevo componente:
>>> # John Lennon, Paul McCartney, George Harrison y Ringo Starr
>>> beatles = set(['Lennon', 'McCartney', 'Harrison', 'Starr'])
>>> beatles.add('Best') # Pete Best
>>> beatles
{'Best', 'Harrison', 'Lennon', 'McCartney', 'Starr'}
Ejecución paso a paso a través de Python Tutor:
Truco
Una pequeña regla mnemotécnica para diferenciar add() de append() es que la función append() significa añadir al final, y como los conjuntos no mantienen un orden, esta función se aplica únicamente a listas. Por descarte, la función add() se aplica sobre conjuntos.
Este pequeño fragmento de código nos demuestra claramente que, aunque lo intentemos por fuerza bruta, nunca vamos a poder insertar elementos repetidos en un conjunto:
>>> items = set()
>>> for _ in range(1_000_000):
... items.add(1)
...
>>> items
{1}
Ejercicio
pycheck: tupleset
Objetos hashables¶
Los elementos de un conjunto deben ser «hashables».
Por ejemplo, una lista no podría ser un objeto válido para un conjunto (ya que no es «hashable»). Supongamos que estamos contruyendo un conjunto con los elementos químicos de la tabla periódica:
>>> periodic_table = set()
>>> metals = ['Fe', 'Mg', 'Au', 'Au', 'Zn']
>>> periodic_table.add(metals)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: unhashable type: 'list'
Sin embargo, podríamos conseguir lo que buscamos si, en vez de listas, usáramos tuplas para almacenar los elementos químicos (ya que sí son «hashables»):
>>> periodic_table = set()
>>> metals = ('Fe', 'Mg', 'Au', 'Au', 'Zn')
>>> periodic_table.add(metals)
>>> non_metals = ('C', 'H', 'O', 'F', 'Cl')
>>> periodic_table.add(non_metals)
>>> periodic_table
{('Fe', 'Mg', 'Au', 'Au', 'Zn'), ('C', 'H', 'O', 'F', 'Cl')}
Borrar elementos¶
Para borrar un elemento de un conjunto podemos utilizar la función remove(). Siguiendo con el ejemplo anterior, vamos a borrar al último «beatle» añadido:
>>> beatles
{'Best', 'Harrison', 'Lennon', 'McCartney', 'Starr'}
>>> beatles.remove('Best')
>>> beatles
{'Harrison', 'Lennon', 'McCartney', 'Starr'}
Si tratamos de borrar un elemento que no existe en un conjunto obtendremos un KeyError (al estilo de los diccionarios):
>>> beatles.remove('Sinatra')
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
KeyError: 'Sinatra'
Longitud de un conjunto¶
Podemos conocer el número de elementos (cardinalidad) que tiene un conjunto con la función len():
>>> beatles
{'Harrison', 'Lennon', 'McCartney', 'Starr'}
>>> len(beatles)
4
Ejercicio
pycheck: diverse_word
Iterar sobre un conjunto¶
Tal y como hemos visto para otros tipos de datos iterables, la forma de recorrer los elementos de un conjunto es utilizar la sentencia for:
>>> for beatle in beatles:
... print(beatle)
...
Harrison
McCartney
Starr
Lennon
Consejo
Como en el ejemplo anterior, es muy común utilizar una variable en singular para recorrer un iterable (en plural). No es una regla fija ni sirve para todos los casos, pero sí suele ser una buena práctica.
Pertenencia de un elemento¶
Al igual que con otros tipos de datos, Python nos ofrece el operador in para determinar si un elemento pertenece a un conjunto:
>>> beatles
{'Harrison', 'Lennon', 'McCartney', 'Starr'}
>>> 'Lennon' in beatles
True
>>> 'Fari' in beatles
False
Obviamente también disponemos de la «negación» del operador:
>>> 'Fari' not in beatles
True
Ejercicio
pycheck: half_out
Ordenando un conjunto¶
Ya hemos comentado que los conjuntos no mantienen un orden. ¿Pero qué ocurre si intentamos ordenarlo?
>>> marks = {8, 4, 6, 2, 9, 5}
>>> sorted(marks)
[2, 4, 5, 6, 8, 9]
Obtenemos una lista con los elementos ordenados.
Hay que tener en cuenta que, lógicamente, no podremos hacer uso de la función sort() sobre un conjunto:
>>> marks.sort()
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
AttributeError: 'set' object has no attribute 'sort'
Teoría de conjuntos¶
Vamos a partir de dos conjuntos \(A=\{1,2\}\) y \(B=\{2,3\}\) para ejemplificar las distintas operaciones que se pueden hacer entre ellos basadas en los Diagramas de Venn y la Teoría de Conjuntos:
>>> A = {1, 2}
>>> B = {2, 3}

Diagramas de Venn¶
Intersección¶
\(A \cap B\) – Elementos que están a la vez en \(A\) y en \(B\):

>>> A & B
{2}
>>> A.intersection(B)
{2}
Unión¶
\(A \cup B\) – Elementos que están tanto en \(A\) como en \(B\):
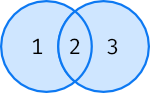
>>> A | B
{1, 2, 3}
>>> A.union(B)
{1, 2, 3}
Diferencia¶
\(A \setminus B\) – Elementos que están en \(A\) y no están en \(B\):
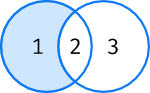
>>> A - B
{1}
>>> A.difference(B)
{1}
Diferencia simétrica¶
\(A \triangle B\) – Elementos que están en \(A\) o en \(B\) pero no en ambos conjuntos:
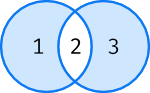
>>> A ^ B
{1, 3}
>>> A.symmetric_difference(B)
{1, 3}
Podemos comprobar que la definición de la diferencia simétrica se cumple también en Python:
>>> A ^ B == (A | B) - (A & B)
True
Inclusión¶
Un conjunto \(B\) es un subconjunto de otro conjunto \(A\) si todos los elementos de \(B\) están incluidos en \(A\).
Un conjunto \(A\) es un superconjunto de otro conjunto \(B\) si todos los elementos de \(B\) están incluidos en \(A\).
Veamos un ejemplo con los siguientes conjuntos:
>>> A = {2, 4, 6, 8, 10}
>>> B = {4, 6, 8}
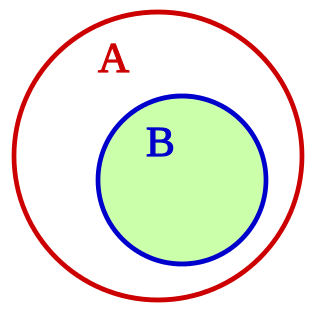
Subconjuntos y Superconjuntos¶
En Python podemos realizar comprobaciones de inclusión (subconjuntos y superconjuntos) utilizando operadores clásicos de comparación:
\(B \subset A\)
>>> B < A # subconjunto
True
\(B \subseteq A\)
>>> B <= A
True
\(A \supset B\)
>>> A > B # superconjunto
True
\(A \supseteq B\)
>>> B >= A
True
El hecho de que algunos elementos sí pertenezcan a otro conjunto no hace que sea un subconjunto. En el siguiente ejemplo tanto \(3\) como \(5\) del conjunto \(B\) están en el conjunto \(A\), pero al no estar el elemento \(1\) no se trata de un subconjunto:
>>> A = {3, 5, 7, 9}
>>> B = {1, 3, 5}
>>> B < A
False
Conjuntos por comprensión¶
Los conjuntos, al igual que las listas y los diccionarios, también se pueden crear por comprensión.
Veamos un ejemplo en el que construimos un conjunto por comprensión con aquellos números enteros múltiplos de 3 en el rango \([0, 20)\):
>>> m3 = {number for number in range(0, 20) if number % 3 == 0}
>>> m3
{0, 3, 6, 9, 12, 15, 18}
Ejercicio
pycheck: common_consonants
Conjuntos inmutables¶
Python ofrece la posibilidad de crear conjuntos inmutables haciendo uso de la función frozenset() que recibe cualquier iterable como argumento.
Supongamos que recibimos una serie de calificaciones de exámenes y queremos crear un conjunto inmutable con los posibles niveles (categorías) de calificaciones:
>>> marks = [1, 3, 2, 3, 1, 4, 2, 4, 5, 2, 5, 5, 3, 1, 4]
>>> marks_levels = frozenset(marks)
>>> marks_levels
frozenset({1, 2, 3, 4, 5})
Veamos qué ocurre si intentamos modificar este conjunto:
>>> marks_levels.add(50)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
AttributeError: 'frozenset' object has no attribute 'add'
Un ejemplo en el que podemos aplicar un «frozenset» sería el conjunto de posibles piezas del ajedrez. Sabemos que estas piezas siempre son las mismas:
>>> CHESS_PIECES = frozenset(('King', 'Queen', 'Bishop', 'Knight', 'Rook', 'Pawn'))
>>> CHESS_PIECES
frozenset({'Bishop', 'King', 'Knight', 'Pawn', 'Queen', 'Rook'})
Nota
Los frozenset son a los sets lo que las tuplas a las listas: una forma de «congelar» los valores para que no se puedan modificar.
EJERCICIOS DE REPASO
pycheck: is_binary
AMPLIAR CONOCIMIENTOS