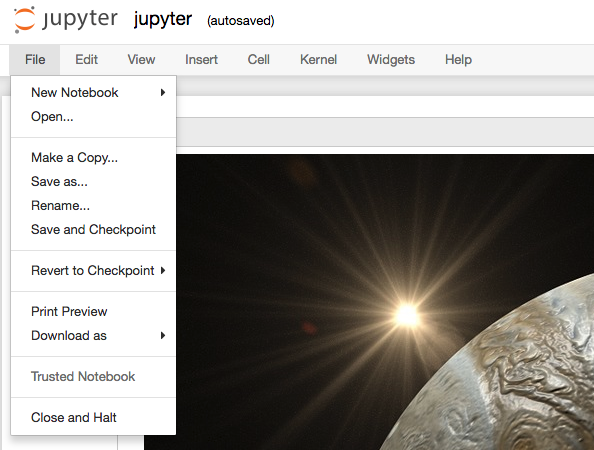
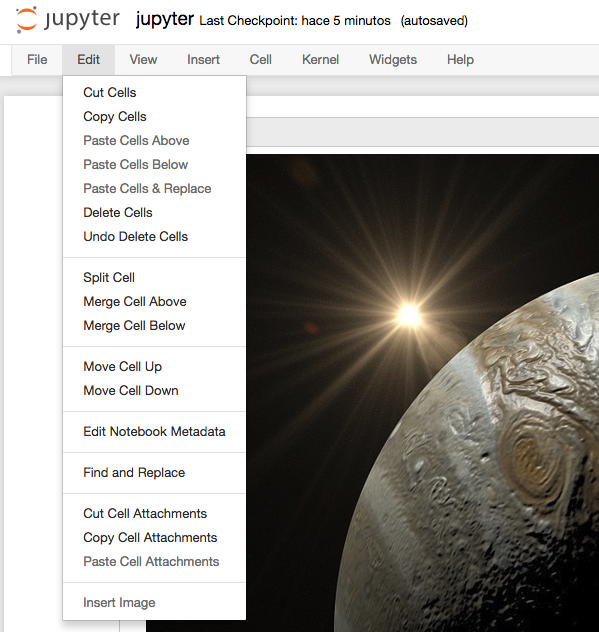
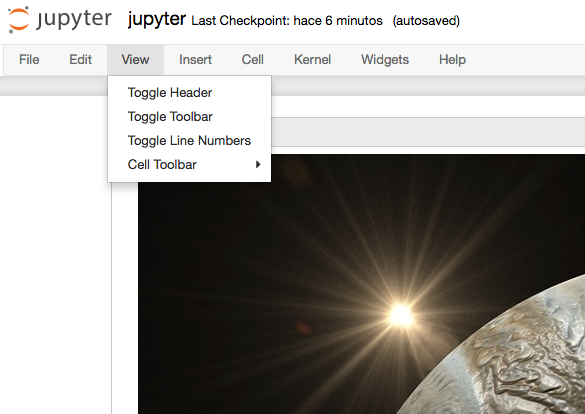
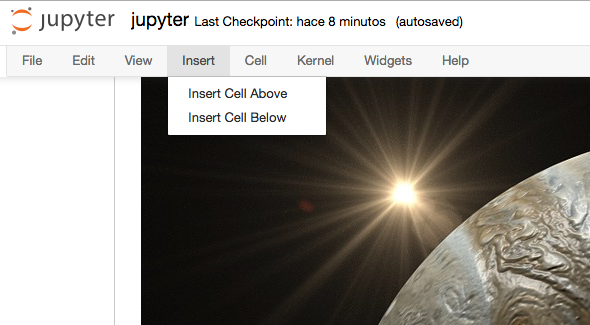
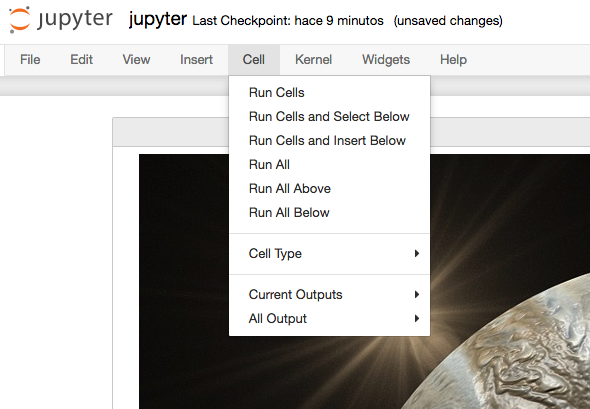
jupyter

../../../_images/nasa-0DjOJ6Q8wUs-unsplash.jpg

El módulo jupyter proporciona un entorno de desarrollo integrado para ciencia de datos, que no es exclusivo de Python, sino que además admite otros lenguajes en su «backend». 1

$ pip install jupyter

Para lanzar el servidor de «notebooks»2:

$ jupyter notebook

Nota

Este comando nos debería abrir una ventana en el navegador web por defecto del sistema, apuntando a la dirección http://localhost:8888

Notebooks

Un «notebook» es un documento que está compuesto por celdas en las que podemos incluir:

  • Texto en formato markdown (incluyendo fórmulas).

  • Elementos multimedia.

  • Código Python ejecutable.

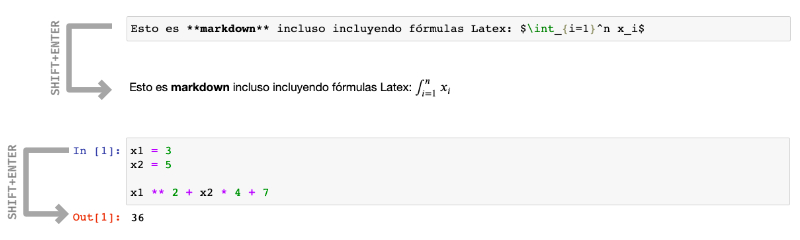
../../../_images/jupyter-cells.jpg

Ejecución de celdas en Jupyter Notebook

En código «markdown», la salida de la celda es la renderización del texto. En código Python, la salida de la celda es el resultado de la última sentencia incluida en la celda.

Nota

Los «notebooks» o cuadernos son básicamente archivos de texto en formato json con extensión .ipynb (que proviene de «IPython Notebook»).

Interfaz

Jupyter se presenta como una aplicación web en cuya interfaz podemos encontrar distintos elementos que nos permitirán desarrollar nuestras tareas de programación de una forma más cómoda.

Explorador de archivos

Lo primero que veremos al arrancar el servidor de «notebooks» será el explorador de archivos con un diseño muy similar al de cualquier sistema operativo.

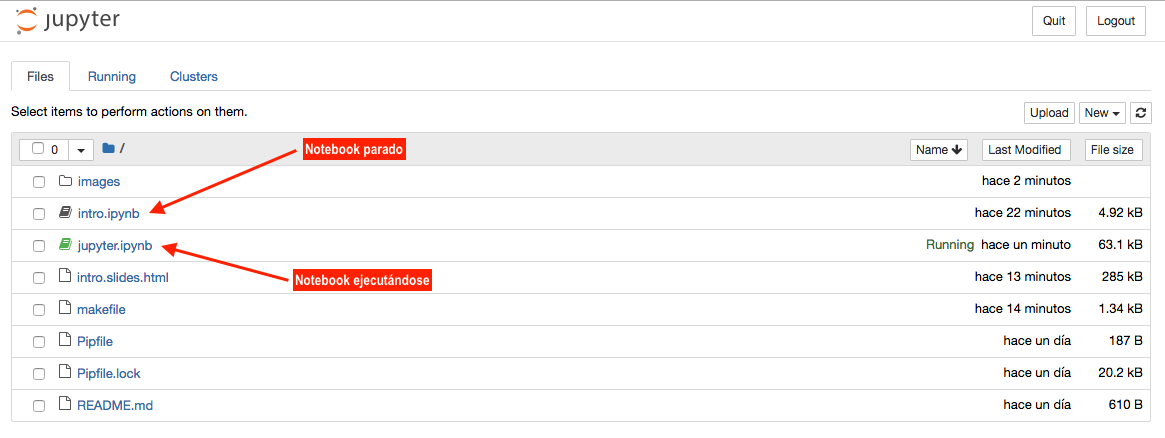
../../../_images/jupyter-browser.png

Explorador de archivos de Jupyter Notebook

Nota

Los «notebooks» que se están ejecutando suelen tener un color verde en el icono, mientras que los que están parados aparecen en gris.

Barra de menú

MathJax

MathJax es una biblioteca javascript que permite visualizar fórmulas matemáticas en navegadores web, utilizando (entre otros) el lenguajes de marcado LaTeX. Para escribir fórmulas matemáticas la celda debe ser de tipo Markdown y tendremos que usar delimitadores especiales.

Fórmulas «en línea»:

Se debe usar el delimitador dólar antes y después de la expresión $ ... $

Por ejemplo: $ \sum_{x=1}^n sin(x) + cos(x) $ produce :\(\sum_{x=1}^n sin(x) + cos(x)\)

Fórmulas «de bloque»:

Se debe usar el delimitador doble dólar antes y después de la expresión $$ ... $$

Por ejemplo: $$ \sum_{x=1}^n sin(x) + cos(x) $$ produce:

\[\sum_{x=1}^n sin(x) + cos(x)\]

Ejemplos de fórmulas

A continuación veremos distintas fórmulas inspiradas en Motivating Examples de la documentación oficial de Jupyter Notebook. Nótese que aunque no se estén indicando los delimitadores $$ sí habría que ponerlos para conseguir el efecto deseado.

Ecuaciones en varias líneas:

\dot{x} = \sigma(y-x) \\
\dot{y} = \rho x - y - xz \\
\dot{z} = -\beta z + xy
\[\begin{split}\dot{x} = \sigma(y-x) \\ \dot{y} = \rho x - y - xz \\ \dot{z} = -\beta z + xy\end{split}\]

Ecuaciones en varias líneas (con alineación):

\begin{align}
    \dot{x} &= \sigma(y-x) \\
    \dot{y} &= \rho x - y - xz \\
    \dot{z} &= -\beta z + xy
\end{align}
\[\begin{split}\dot{x} &= \sigma(y-x) \\ \dot{y} &= \rho x - y - xz \\ \dot{z} &= -\beta z + xy\end{split}\]

Usando paréntesis:

\left( \sum_{k=1}^n a_k b_k \right)^2 \leq
\left( \sum_{k=1}^n a_k^2 \right) \left( \sum_{k=1}^n b_k^2 \right)
\[\left( \sum_{k=1}^n a_k b_k \right)^2 \leq \left( \sum_{k=1}^n a_k^2 \right) \left( \sum_{k=1}^n b_k^2 \right)\]

Trabajando con matrices:

\mathbf{V}_1 \times \mathbf{V}_2 =
\begin{vmatrix}
    \mathbf{i} & \mathbf{j} & \mathbf{k} \\
    \frac{\partial X}{\partial u} &  \frac{\partial Y}{\partial u} & 0 \\
    \frac{\partial X}{\partial v} &  \frac{\partial Y}{\partial v} & 0
\end{vmatrix}
\[\begin{split}\mathbf{V}_1 \times \mathbf{V}_2 = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial X}{\partial u} & \frac{\partial Y}{\partial u} & 0 \\ \frac{\partial X}{\partial v} & \frac{\partial Y}{\partial v} & 0 \end{vmatrix}\end{split}\]

Algo de probabilidad:

P(E) = {n \choose k} p^k (1-p)^{ n-k}
\[P(E) = {n \choose k} p^k (1-p)^{ n-k}\]

Algunos ejemplos con fracciones:

\frac{1}{\Bigl(\sqrt{\phi \sqrt{5}}-\phi\Bigr) e^{\frac25 \pi}} =
1+\frac{e^{-2\pi}} {1+\frac{e^{-4\pi}} {1+\frac{e^{-6\pi}}
{1+\frac{e^{-8\pi}} {1+\ldots} } } }
\[\frac{1}{\Bigl(\sqrt{\phi \sqrt{5}}-\phi\Bigr) e^{\frac25 \pi}} = 1+\frac{e^{-2\pi}} {1+\frac{e^{-4\pi}} {1+\frac{e^{-6\pi}} {1+\frac{e^{-8\pi}} {1+\ldots} } } }\]
1 +  \frac{q^2}{(1-q)}+\frac{q^6}{(1-q)(1-q^2)}+\cdots =
\prod_{j=0}^{\infty}\frac{1}{(1-q^{5j+2})(1-q^{5j+3})},
\quad\quad \text{for $|q|<1$}.
\[1 + \frac{q^2}{(1-q)}+\frac{q^6}{(1-q)(1-q^2)}+\cdots = \prod_{j=0}^{\infty}\frac{1}{(1-q^{5j+2})(1-q^{5j+3})}, \quad\quad \text{for $|q|<1$}.\]

Múltiples puntos de alineación:

\begin{eqnarray}
    x' &=&   &x \sin\phi &+& z \cos\phi \\
    z' &=& - &x \cos\phi &+& z \sin\phi
\end{eqnarray}
\[ \begin{array}{ccccccc} x' &=& &x \sin\phi &+& z \cos\phi \\ z' &=& - &x \cos\phi &+& z \sin\phi \end{array} \]

Ejercicio

Escriba en MathJax las siguientes ecuaciones:

Ecuación 1

\[\int_a^b f'(x)dx = f(b) - f(a)\]

Ecuación 2

\[t' = t \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}\]

Ecuación 3

\[\Big[ M \frac{\partial}{\partial M} + \beta(g) \frac{\partial}{\partial g} + \eta \gamma \Big] G^n(x_1, x_2, \dots, x_n; M, g) = 0\]

Ecuación 4

\[R_{00} \approx -\frac{1}{2} \sum_i \frac{\partial^2 h_{00}}{\partial(x^i)^2} = \frac{4\pi G}{c^2} (\rho c^2) \Rightarrow \bigtriangledown^2 \phi_g = 4\pi G \rho\]

Truco

Puede encontrar símbolos matemáticos para Latex en este enlace así como dibujar directamente un símbolo y obtener su referencia a través de la herramienta Detexify.

Solución: equations.tex

Comandos especiales

Jupyter Notebook ofrece una gama de comandos especiales que cubren gran variedad de funcionalidades.

Comandos de shell

Podemos ejecutar comandos de «shell» usando el prefijo exclamación !

>>> !date
martes, 15 de junio de 2021, 09:13:25 WEST

>>> !whoami
sdelquin

Ejercicio

Ejecute los siguientes comandos del sistema y obtenga la salida en una celda del Notebook:

Windows

Linux & macOS

time

date

dir

ls

mem

free

Obteniendo ayuda

Una de las formas más sencillas de obtener información de librerías, funciones o módulos es utilizar el sufijo interrogación ?

>>> import random

>>> random.randint?
Signature: random.randint(a, b)
Docstring:
Return random integer in range [a, b], including both end points.

File:      ~/.pyenv/versions/3.9.1/lib/python3.9/random.py
Type:      method

Ejercicio

Obtenga la documentación de las siguientes funciones:

  • os.path.dirname

  • re.match

  • datetime.timedelta

Comandos mágicos

Jupyter Notebook, o mejor expresado IPython, admite un conjunto de comandos mágicos que permiten realizar distintas tareas, en muchos casos, no necesariamente relacionadas con Python:

>>> %lsmagic
Available line magics:
%aimport  %alias  %alias_magic  %autoawait  %autocall  %autoindent  %automagic  %autoreload  %bookmark  %cat  %cd  %clear  %colors  %conda  %config  %cp  %cpaste  %debug  %dhist  %dirs  %doctest_mode  %ed  %edit  %env  %gui  %hist  %history  %killbgscripts  %ldir  %less  %lf  %lk  %ll  %load  %load_ext  %loadpy  %logoff  %logon  %logstart  %logstate  %logstop  %ls  %lsmagic  %lx  %macro  %magic  %man  %matplotlib  %mkdir  %more  %mv  %notebook  %page  %paste  %pastebin  %pdb  %pdef  %pdoc  %pfile  %pinfo  %pinfo2  %pip  %popd  %pprint  %precision  %prun  %psearch  %psource  %pushd  %pwd  %pycat  %pylab  %quickref  %recall  %rehashx  %reload_ext  %rep  %rerun  %reset  %reset_selective  %rm  %rmdir  %run  %save  %sc  %set_env  %store  %sx  %system  %tb  %time  %timeit  %unalias  %unload_ext  %who  %who_ls  %whos  %xdel  %xmode

Available cell magics:
%%!  %%HTML  %%SVG  %%bash  %%capture  %%debug  %%file  %%html  %%javascript  %%js  %%latex  %%markdown  %%perl  %%prun  %%pypy  %%python  %%python2  %%python3  %%ruby  %%script  %%sh  %%svg  %%sx  %%system  %%time  %%timeit  %%writefile

Automagic is ON, % prefix IS NOT needed for line magics.

Si nos fijamos en el último mensaje, al estar habilitado el modo «automagic», no es estrictamente necesario que usemos el prefijo % para hacer uso de estos comandos. Por ejemplo, si quisiéramos conocer la historia de comandos en el intérprete:

>>> hist  # equivalente a %hist
!date
import random
random.randint?
%lsmagic
pwd
hist

Representando gráficas

Otra de las grandes ventajas que ofrece Jupyter Notebook es poder graficar directamente sobre el cuaderno. Para ello utilizamos código Python (en este caso) y una directiva de comando mágico para indicar que se renderice en línea:

>>> %matplotlib inline

>>> from matplotlib import pyplot as plt

>>> x = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
>>> y = [1, 4, 9, 16, 25, 36, 49, 64, 81, 100]

>>> plt.plot(x, y)
[<matplotlib.lines.Line2D at 0x106414e50>]
<Figure size 432x288 with 1 Axes>
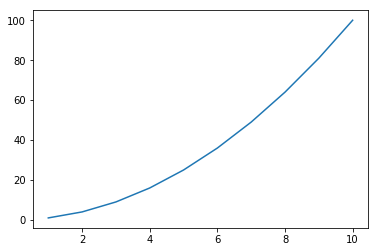
../../../_images/basic-plot.png

Gráfica sencilla hecha en Jupyter Notebook

Manejando ficheros

Cargando un fichero en la celda actual:

Para ello utilizamos el comando %load "ruta/al/fichero"

Ejecutando un fichero en la celda actual:

Para ello utilizamos el comando %run "ruta/al/fichero"

Escribiendo el contenido de la celda actual a fichero:

Para ello utilizamos el comando %writefile "ruta/al/fichero" como primera línea de la celda y después vendría el código que queremos escribir.

Ejercicio

  • En una celda del «notebook», escriba código Python para crear una lista de 100 números pares.

  • Guarde el contenido de esa celda un fichero Python usando %%writefile

  • Carge este fichero en una celda con %load

  • Ejecútelo con %run

Tiempos de ejecución

Para medir el tiempo de ejecución de una determinada instrucción Python podemos utilizar el comando %timeit que calcula un promedio tras correr repetidas veces el código indicado:

>>> import numpy

>>> %timeit numpy.random.normal(size=100)
3.03 µs ± 6.77 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

De igual forma, existe un mecanismo para medir el tiempo de ejecución de una celda completa. En este caso se utiliza el comando %%timeit (nótese la diferencia del doble porcentaje como prefijo):

%%timeit

numpy.random.poisson(size=100)
numpy.random.uniform(size=100)
numpy.random.logistic(size=100)

8.88 µs ± 25.8 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

Ejercicio

Mida si hay diferencias significativas en tiempos de ejecución en la creación de distribuciones aleatorias atendiendo a:

  • Tipo de distribución (Poisson, Uniform, Logistic).

  • Tamaño de la muestra (100, 10000, 1000000).

Solución: timeit.py

Incluyendo otros lenguajes

Celdas con HTML:

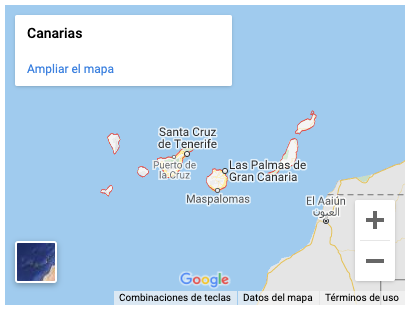
Si necesitamos insertar código HTML en una celda, podemos usar el comando %%html al comienzo de la misma:

%%html

<iframe src="https://www.google.com/maps/embed?pb=!1m18!1m12!1m3!1d3592984.8538165656!2d-18.096789575396794!3d28.426067294993228!2m3!1f0!2f0!3f0!3m2!1i1024!2i768!4f13.1!3m3!1m2!1s0xc41aa86ef755363%3A0x10340f3be4bc8c0!2sCanarias!5e0!3m2!1ses!2ses!4v1623755509663!5m2!1ses!2ses" width="400" height="300" style="border:0;" allowfullscreen="" loading="lazy"></iframe>
../../../_images/canaryislands-googlemaps.png
Celdas con «shell script»:

Hay ocasiones en las que un código en shell script suele ser útil. Para incluirlo recurrimos al comando %%bash al principio de la celda:

%%bash

!tree -d -L 2
.
├── __pycache__
├── _build
│   └── html
├── _static
│   ├── css
│   ├── img
│   └── js
├── core
│   ├── controlflow
│   ├── datastructures
│   ├── datatypes
│   ├── devenv
│   ├── introduction
│   └── modularity
├── miniprojects
│   └── spotify
├── pypi
│   └── datascience
└── stdlib
    └── text_processing

20 directories
Celdas con perl:

No hay que subestimar el poder del lenguaje de programación perl. Si fuera necesario, lo podemos incluir en una celda del «notebook» con %%perl al comienzo de la misma:

%%perl

my $email = 'sdelquin@gmail.com';

if ($email =~ /^([^@]+)\@(.+)$/) {
    print "Username is: $1\n";
    print "Hostname is: $2\n";
}

...

Username is: sdelquin
Hostname is: gmail.com

Extensiones

El ecosistema de Jupyter Notebook es muy amplio y ofrece una gran variedad de extensiones que se pueden incluir en la instalación que tengamos: Unofficial Jupyter Notebook Extensions.

Su instalación es tan sencilla como:

$ pip install jupyter_contrib_nbextensions

Otros entornos

El ecosistema de entornos para trabajos en ciencia de datos ha ido ampliándose durante estos últimos años con la explosión del «BigData» y la inteligencia artificial. En este apartado veremos otras plataformas que también nos permiten usar Python enfocado al análisis de datos.

JupyterLab

JupyterLab es una evolución de Jupyter Notebook. Entre sus mejoras podemos destacar:

  • Explorador de ficheros integrado en la barra lateral.

  • Posibilidad de abrir múltiples .ipynb al mismo tiempo usando pestañas.

  • Posibilidad de abrir múltiples terminales.

  • Editor integrado para cualquier fichero de texto.

  • Vista previa en tiempo real de documentos markdown o csv.

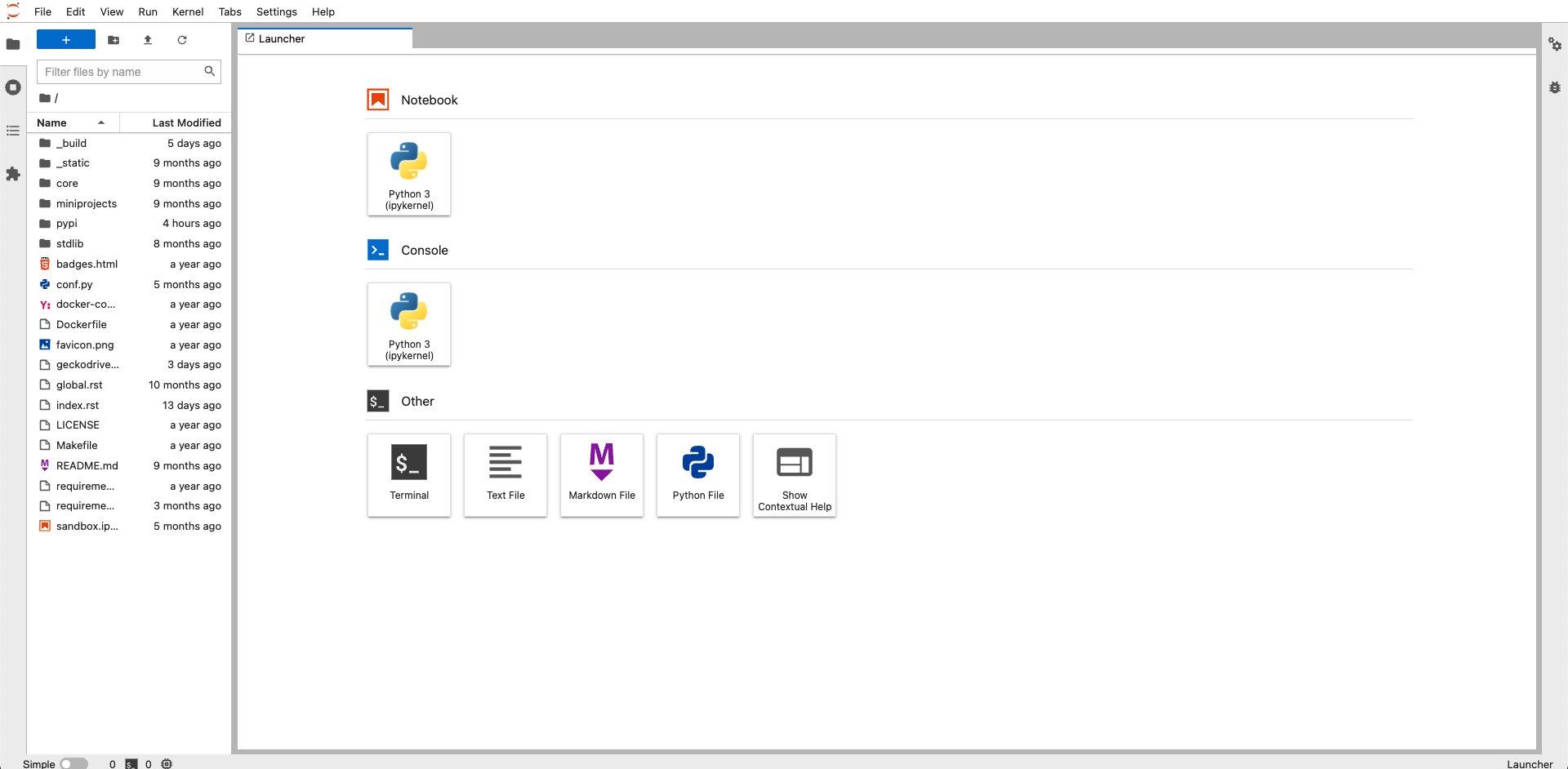
../../../_images/jupyterlab.png

Pantalla inicial de JupyterLab

Su instalación se lleva a cabo como cualquier otro paquete Python:

$ pip install jupyterlab

Para ejecutar la aplicación:

$ jupyter-lab

Google Colab

Google Colab es un entorno de computación científica creado por Google y disponible en su nube. Como era previsible, para su uso es necesario disponer de una cuenta en Google.

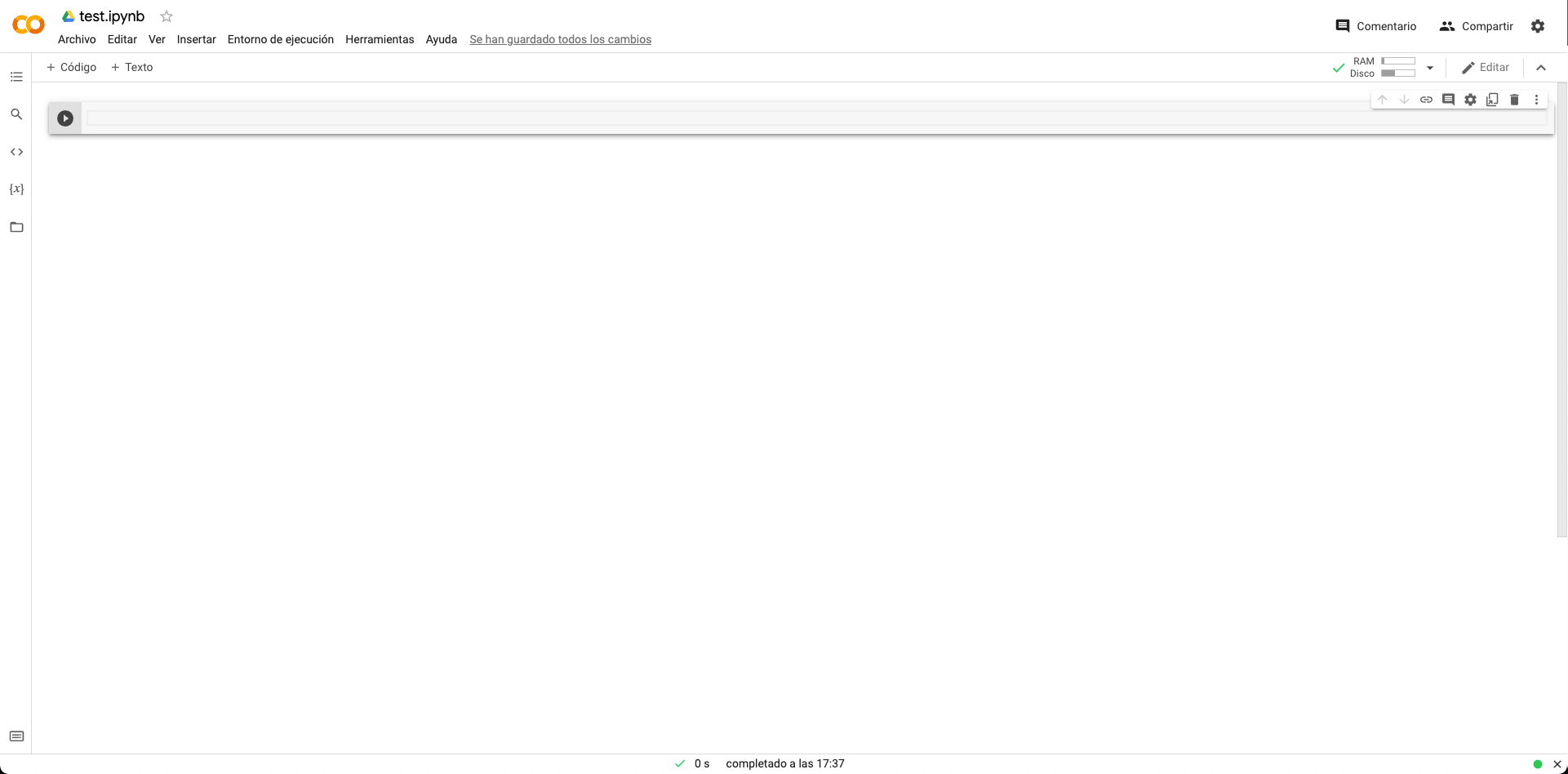
../../../_images/google-colab.png

Pantalla inicial de Google Colab

Características:

  • Tiene un comportamiento totalmente análogo a Jupyter en cuanto a comportamiento y funcionalidades.

  • Completamente en la nube. No necesita instalación ni configuración.

  • Por defecto trae multitud de paquetes instalados, principalmente en el ámbito científico: 386 paquetes (febrero de 2022).

  • Versión de Python: 3.7.12 (febrero de 2022).

  • Espacio en disco sujeto a las características de Google Compute Engine: 107.72GB (febrero de 2022)

  • Memoria RAM sujeta a las características de Google Compute Engine: 12.69GB (febrero de 2022)

  • Acceso limitado al sistema operativo.

  • En cuentas gratuitas, los tiempos de cómputo son, por lo general, mayores que en una máquina local. 4

  • Previsualización markdown en tiempo real sobre cada celda.

  • Posibilidad de subir ficheros de datos propios en carpetas accesibles por el cuaderno.

  • Posibilidad de ejecutar Jupyter «notebooks» propios.

  • Posibilidad (limitada) de acelerar cálculos usando GPU 6 o TPU 7.

  • Posibilidad de descargar el cuaderno como Jupyter «notebook» o archivo de Python.

  • Índice de contenidos integrado en barra lateral.

  • Inspector de variables integrado en barra lateral.

Kaggle

Kaggle es una plataforma que no sólo ofrece un entorno de trabajo para cuadernos Jupyter sino también una enorme colección de conjuntos de datos de libre acceso. Para su uso es necesario disponer de una cuenta en el servicio.

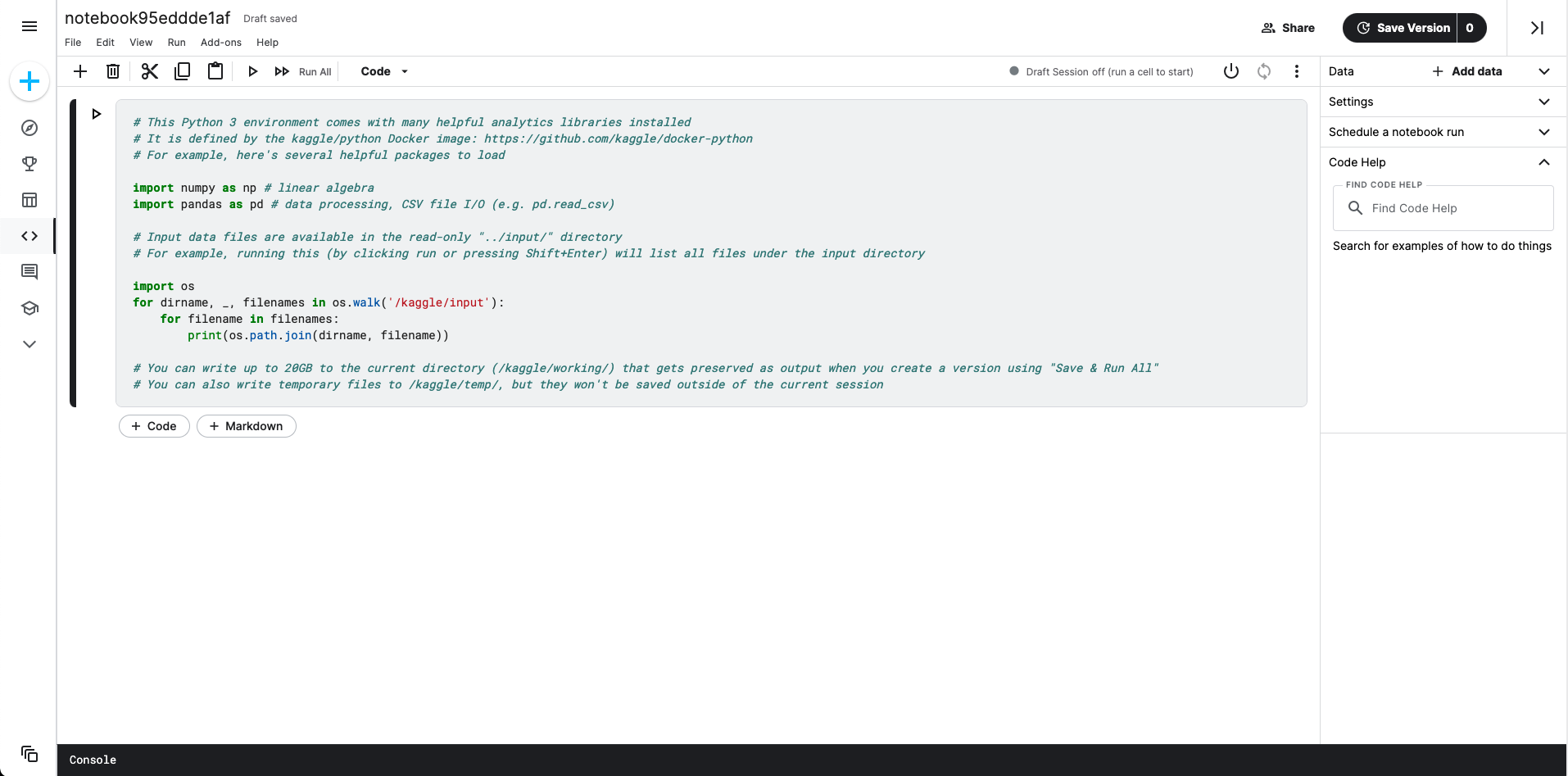
../../../_images/kaggle.png

Pantalla inicial de Kaggle

Características:

  • Tiene un comportamiento totalmente análogo a Jupyter en cuanto a comportamiento y funcionalidades.

  • Completamente en la nube. No necesita instalación ni configuración.

  • Por defecto trae multitud de paquetes instalados, principalmente en el ámbito científico: 792 paquetes (febrero de 2022).

  • Versión de Python: 3.7.12 (febrero de 2022).

  • Espacio en disco sujeto a las características de Kaggle: 73.1GB (febrero de 2022)

  • Memoria RAM sujeta a las características de Kaggle: 16GB (febrero de 2022)

  • Acceso limitado al sistema operativo.

  • En cuentas gratuitas, los tiempos de cómputo son, por lo general, mayores que en una máquina local. 4

  • Posibilidad de subir ficheros de datos propios sólo como «datasets» de Kaggle.

  • Posibilidad de ejecutar Jupyter «notebooks» propios.

  • Posibilidad (limitada) de acelerar cálculos usando GPU 6 o TPU 7.

  • Posibilidad de descargar el cuaderno como Jupyter «notebook».

Comparativa

Haremos una comparativa de tiempos de ejecución lanzando una FFT 5 sobre una matriz de 1 millón de elementos:

>>> import numpy as np

>>> bigdata = np.random.randint(1, 100, size=(1_000, 1_000))

>>> %timeit np.fft.fft(bigdata)
4.89 ms ± 5.78 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

Jupyter

Colab

Kaggle

4.89ms

13.9ms

12.8ms

Obviamente se trata de una ejecución puntual y no podemos sacar conclusiones claras al respecto. Además de ello depende del «hardware» sobre el que estemos trabajando. En cualquier caso el propósito es únicamente tener una ligera idea de los órdenes de magnitud.

1

Foto original de portada por NASA en Unsplash.

2

Un «notebook» es el concepto de cuaderno (documento) científico que se maneja en Jupyter

3

Un «shortcut» es un «atajo de teclado» (combinación de teclas) para lanzar una determinada acción.

4(1,2)

Todo estará en función de las características de la máquina con la que se esté trabajando.

5

Fast Fourier Transform (Transformada rápida de Fourier).

6(1,2)

Graphics Processing Unit (Unidad gráfica de procesamiento).

7(1,2)

Tensor Processing Unit (Unidad de procesamiento tensorial).